I. Introduction▲
La cryptographie a évolué en trois périodes historiques.
- La cryptographie mécanique. Il s'agit de la cryptographie qui utilise des moyens mécaniques pour chiffrer un message. Cette cryptographie s'étend de l'antiquité jusqu'à la fin de la Seconde Guerre mondiale environ. De nos jours, elle n'a plus cours.
- La cryptographie mathématique. Il s'agit de la cryptographie qui utilise les mathématiques pour chiffrer un message. Cette cryptographie a commencé aux environs de la fin de la Deuxième Guerre mondiale et c'est celle que l'on utilise de nos jours.
- La cryptographie quantique. Il s'agit de la cryptographie dont les bases reposent sur la physique quantique. Nous sommes en train de la voir émerger de nos jours et nul doute qu'elle ne remplace dans les années qui viennent la cryptographie basée sur les mathématiques.
Cette présentation ne veut pas être une référence complète dans laquelle tous les détails très techniques sont explicités. Le but de ce document est de fournir suffisamment de pistes au lecteur qui voudrait approfondir certains détails.
Cette pr√©sentation n'est pas forc√©ment compl√®te non plus, certains points (les diff√©rentes m√©thodes de cryptanalyse par exemple) ont √©t√© volontairement laiss√©s de c√īt√©.
N'hésitez pas à me contacter par messagerie privée si vous constatez une faute d'orthographe, une erreur dans mes explications, une omission dans les thèmes abordés ou bien un détail difficilement compréhensible, je vous en remercie d'avance et les futurs lecteurs aussi.
II. Terminologie▲
Dans cette présentation je m'attacherai à utiliser toujours les mêmes termes. Ce paragraphe présente les termes utilisés ainsi que leur signification.
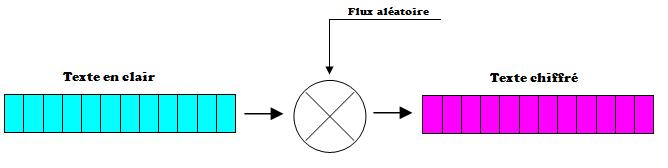
- Texte en clair : c'est le message à protéger.
- Texte chiffré : c'est le résultat du chiffrement du texte en clair.
- Chiffrement : c'est la méthode ou l'algorithme utilisé pour transformer un texte en clair en texte chiffré.
- Déchiffrement c'est la méthode ou l'algorithme utilisé pour transformer un texte chiffré en texte en clair.
- Clé : c'est le secret partagé utilisé pour chiffrer le texte en clair en texte chiffré et pour déchiffrer le texte chiffré en texte en clair. On peut parfaitement concevoir un algorithme qui n'utilise pas de clé, dans ce cas c'est l'algorithme lui-même qui constitue la clé, et son principe ne doit donc en aucun cas être dévoilé.
- Cryptographie : cette branche regroupe l'ensemble des méthodes qui permettent de chiffrer et de déchiffrer un texte en clair afin de le rendre incompréhensible pour quiconque n'est pas en possession de la clé à utiliser pour le déchiffrer.
- Cryptanalyse¬†: c'est l'art de r√©v√©ler les textes en clair qui ont fait l'objet d'un chiffrement sans conna√ģtre la cl√© utilis√©e pour chiffrer le texte en clair.
- Cryptologie : il s'agit de la science qui étudie les communications secrètes. Elle est composée de deux domaines d'étude complémentaires : la cryptographie et la cryptanalyse.
- Décrypter : c'est l'action de retrouver le texte en clair correspondant à un texte chiffré sans posséder la clé qui a servi au chiffrement. Ce mot ne devrait donc être employé que dans le contexte de la cryptanalyse.
- Crypter : en relisant la définition du mot décrypter, on peut se rendre compte que le mot crypter n'a pas de sens et que son usage devrait être oublié. Le mot cryptage n'a pas plus de sens non plus.
- Coder, décoder : c'est une méthode ou un algorithme permettant de modifier la mise en forme d'un message sans introduire d'élément secret. Le Morse est donc un code puisqu'il transforme des lettres en trait et points sans notion de secret. L'ASCII est lui aussi un code puisqu'il permet de transformer une lettre en valeur binaire.
III. Cryptographie historique▲
Ce paragraphe pr√©sente plusieurs algorithmes ou m√©thodes de cryptographie √† une √©poque o√Ļ les math√©matiques ne r√©gnaient pas encore en ma√ģtres sur ce domaine.
III-A. La technique grecque▲
Une m√©thode de chiffrement dat√©e entre le Xe et VIIe si√®cle avant J√©sus Christ repose sur l'utilisation d'un b√Ęton appel√© scytale d'un diam√®tre fix√©. Une lani√®re en cuir √©tait enroul√©e en h√©lice autour de ce b√Ęton et le texte en clair √©tait alors √©crit sur la lani√®re. Ensuite, la lani√®re √©tait d√©roul√©e et pouvait √™tre envoy√©e (sans le b√Ęton) au destinataire du message.

Pour d√©chiffrer le texte chiffr√©, il suffisait d'utiliser un b√Ęton poss√©dant exactement le m√™me diam√®tre que le pr√©c√©dent, d'y enrouler la lani√®re de cuir et le texte en clair pouvait alors √™tre relu.
Le procédé utilisé par cette méthode est un chiffrement par transposition, c'est-à-dire que les lettres ne sont pas modifiées, mais que seul l'ordre des lettres est changé.
III-B. Le code de C√©sar▲
Le code de César est une méthode connue par tous les écoliers. Il suffit de décaler les lettres d'un certain nombre connu aussi bien par celui qui écrit le message que par celui qui le reçoit.
Par exemple si n=4, cela donne :
- a=E, b=F, c=G… w=À, x=B, y=C, z=D.
Si le texte en clair √† chiffrer est ¬ę¬†rendons a cesar ce qui est a cesar¬†¬Ľ, avec un d√©calage de quatre lettres, le texte chiffr√© est ¬ę¬†VIRHSRW E GIWEV GI UYM IWX E GIWEV¬†¬Ľ.
Ce procédé est un procédé de chiffrement par substitution monoalphabétique. Il est très simple, mais il ne résiste pas à une analyse basée sur la fréquence des caractères puisque chaque lettre est toujours remplacée par la même lettre. D'ailleurs dans l'exemple fourni, le mot cesar est chiffré deux fois de la même manière en GIWEV de même que le a est chiffré deux fois en E.
Un autre algorithme, nommé ROT13, basé sur le même fonctionnement a existé au tout début de l'informatique. Le décalage était de treize lettres, et c'est donc le même algorithme qui était utilisé aussi bien pour le chiffrement que pour le déchiffrement (un premier décalage de treize lettres pour chiffrer suivi d'un autre décalage de treize lettres pour déchiffrer suffisait à redonner le texte en clair).
III-C. Le code de Vigen√®re▲
Le code de Vigenère est présenté pour la première fois par le diplomate Blaise de Vigenère au courant du XVIe siècle.
Il reprend pour cela le principe du code de César, mais il le complexifie en introduisant la notion de décalage variable en fonction d'une clé. Le code de Vigenère repose d'abord sur le carré de Vigenère. Il s'agit de l'alphabet qui est répété sur 26 lignes, mais décalé d'une lettre à chaque fois.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z A B C D E F G H I J K L M N O P Q R S T U V W X YIl nécessite ensuite un mot clé seulement connu par l'émetteur et le destinataire du message. C'est le premier algorithme à introduire la notion de clé. Ce mot clé est répété autant de fois que nécessaire afin d'avoir autant de lettres (ou plus) que le texte en clair à chiffrer. Ensuite l'alphabet utilisé pour chiffrer une lettre est celui correspondant à la lettre du mot clé.
Si le texte √† chiffrer est ¬ę¬†rendons a vigenere ce qui est a vigenere¬†¬Ľ, avec le mot cl√© ¬ę¬†RAYMOND¬†¬Ľ, le texte chiffr√© est ¬ę¬†IELPCAV R VGSSAHIE AQ EHL VSR M JVJVNCDS¬†¬Ľ.
rendons a vigenere ce qui est a vigenere
RAYMONDRAYMONDRAYMONDRAYMONDRAYMONDRAYMOND
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Alphabet à utiliser pour la lettre A de la clé
B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D E F G H I J K L M N O P Q R S T U V W X Y Z A B C Alphabet à utiliser pour la lettre D de la clé
E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M N O P Q R S T U V W X Y Z A B C D E F G H I J K L Alphabet à utiliser pour la lettre N de la clé
N O P Q R S T U V W X Y Z A B C D E F G H I J K L M Alphabet à utiliser pour la lettre N de la clé
O P Q R S T U V W X Y Z A B C D E F G H I J K L M N Alphabet à utiliser pour la lettre O de la clé
P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R S T U V W X Y Z A B C D E F G H I J K L M N O P Q Alphabet à utiliser pour la lettre R de la clé
S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T U V W X Y Z A B C D E F G H I J K L M N O P Q R S
U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y Z A B C D E F G H I J K L M N O P Q R S T U V W X Alphabet à utiliser pour la lettre Y de la clé
Z A B C D E F G H I J K L M N O P Q R S T U V W X YDans cet exemple on voit que les deux mots vigenere ne sont plus codés de la même manière (VGSSAHIE et JVJVNCDS) de même pour la lettre a qui est codée en R et M.
Ce code ne sera cassé qu'en 1854 (soit 200 ans plus tard) par le mathématicien Charles Babbage.
III-D. La machine Enigma▲
La machine Enigma est née en 1918 dans l'entreprise de l'inventeur Arthur Scherbius en Allemagne. Elle a été utilisée par l'armée allemande durant la Seconde Guerre mondiale.
Il s'agit d'une machine à chiffrer et à déchiffrer mécanique qui allie à la fois les méthodes de substitution et de transposition.
Cette machine se compose de :
- un tableau de connexion qui permet d'échanger 6 paires de lettres 2 à 2 ;
- trois rotors choisis parmi les six rotors existants. Chaque rotor comprend 26 positions différentes. La position du premier rotor avance avec chaque lettre. Au bout de 26 lettres et donc 26 décalages, le premier rotor est revenu à sa position initiale et c'est le second rotor qui avance d'une lettre et ainsi de suite ;
- un réflecteur qui permet de repasser la lettre en cours de chiffrage dans les rotors et dans le tableau de connexion.
Le nombre de clés possibles est le suivant :
- choix de 6 paires de lettres parmi 26 lettres = 100 391 791 500 possibilités
- choix de 3 rotors parmi 6 = 120 possibilités
- choix de la position initiale des 3 rotors parmi les 26 positions possibles = 26 * 26 * 26 = 17 576 possibilités
- Ce qui fait un nombre total de 211 738 335 288 480 000 clés différentes.
Le code utilisé par la machine Enigma sera lui aussi cassé durant la Seconde Guerre mondiale. Les Polonais avant et au tout début de la Seconde Guerre mondiale auront commencé le travail de compréhension de l'algorithme. Les Anglais à Bletchley Park avec l'aide d'Alan Turing finiront le travail.
III-E. Conclusion▲
Bien s√Ľr, il y a eu de nombreux autres codes utilisant des variations sur ces codes ou alors de nouveaux concepts. Mais la plupart des proc√©d√©s cryptographiques reposent essentiellement sur deux moyens¬†:
- la transposition, l'ordre des lettres du message est modifié dans le message ;
- la substitution, les lettres sont remplacées par d'autres lettres selon une certaine règle.
En ce qui concerne la substitution, il faut noter qu'il y en a plusieurs :
- substitution monoalphabétique : chaque lettre du message est remplacée par une autre lettre de l'alphabet. Le code de César utilise cette technique ;
- substitution polyalphabétique : chaque lettre du message est remplacée par une autre lettre d'un alphabet indiqué par une lettre de la clé. Le code de Vigenère utilise cette technique ;
- substitution homophonique : chaque lettre du message est remplacée par une des lettres de substitution possibles. Le nombre de lettres de substitution possibles est fonction de la fréquence de la lettre dans le langage concerné. Cette méthode de substitution a pour but d'empêcher le déchiffrage du message par une analyse fréquentielle ;
- substitution polygramme : chaque groupe de caractères est remplacé par un autre groupe de caractères.
IV. La st√©ganographie▲
La stéganographie n'est pas vraiment une méthode cryptographique. Elle repose sur le fait que l'information à cacher est mélangée avec de l'information banale de manière à passer inaperçue.
IV-A. Le texte cach√©▲
Un grand classique de la stéganographie est cet échange de lettres entre George Sand et Alfred de Musset (cet échange fut-il réel ou bien fait-il partie des légendes urbaines du Web, je ne sais pas, mais le contenu est tout de même beau) :
Je suis très émue de vous dire que j'ai
bien compris l'autre soir que vous aviez
toujours une envie folle de me faire
danser. Je garde le souvenir de votre
baiser et je voudrais bien que ce soit
là une preuve que je puisse être aimée
par vous. Je suis prête à vous montrer mon
affection toute désintéressée et sans cal-
cul, et si vous voulez me voir aussi
vous d√©voiler sans artifice mon √Ęme
toute nue, venez me faire une visite.
Nous causerons en amis, franchement.
Je vous prouverai que je suis la femme
sincère, capable de vous offrir l'affection
la plus profonde comme la plus étroite
en amitié, en un mot la meilleure preuve
dont vous puissiez rêver, puisque votre
√Ęme est libre. Pensez que la solitude o√Ļ j'ha-
bite est bien longue, bien dure et souvent
difficile. Ainsi en y songeant j'ai l'√Ęme
grosse. Accourrez donc vite et venez me la
faire oublier par l'amour o√Ļ je veux me
mettre.La réponse d'Alfred de Musset :
Quand je mets à vos pieds un éternel hommage
Voulez-vous qu'un instant je change de visage ?
Vous avez captur√© les sentiments d'un cŇďur
Que pour vous adorer forma le Créateur.
Je vous chéris, amour, et ma plume en délire
Couche sur le papier ce que je n'ose dire.
Avec soin, de mes vers lisez les premiers mots
Vous saurez quel remède apporter à mes maux.Et enfin la réponse de George Sand :
Cette insigne faveur que votre cour réclame
Nuit √† ma renomm√©e et r√©pugne mon √Ęme.Et vous, saurez-vous retrouver le message cach√© dans cet √©change de lettres (la solution se trouve √† la fin de ce document dans les annexes)¬†?
IV-B. La st√©ganographie dans les fichiers images▲
De la m√™me mani√®re que pour le texte, il est possible de cacher de l'information dans des fichiers images. En modifiant ou alt√©rant quelques bits du fichier, il est ainsi possible de cacher un copyright ou alors un message de son choix sans que cela se voie. En effet, cette alt√©ration sera peu ou pas visible, car l'Ňďil humain n'est pas capable de discerner des petites aberrations sur une grande image √† condition que le ratio taille du message / taille de l'image ne soit pas trop grand.
IV-C. Un canal cach√© dans le protocole ICMP▲
Le protocole ICMP est un protocole utilis√© pour contr√īler le fonctionnement d'un r√©seau IP. Une des applications la plus connue est l'utilitaire ping qui permet de conna√ģtre la pr√©sence ou non d'une machine sur le r√©seau.
Le format d'une trame ICMP est le suivant :
0 1 2 3
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Type | Code | Checksum |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Identificateur | Numéro de Séquence |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Data ...
+-+-+-+-+-Pour les trames ICMP echo request et ICMP echo reply qui sont les trames générées et reçues par l'utilitaire ping, les valeurs des différents champs sont les suivantes :
- Type : 8 pour un message echo request et 0 pour un message echo reply.
- Code : toujours 0.
- Checksum¬†: Ce champ est la somme de contr√īle de la trame ICMP.
- Identificateur : Il s'agit d'un nombre utilisé pour aider à repérer les réponses.
- Numéro de séquence : Il s'agit d'un nombre utilisé pour aider à repérer les réponses.
- Data : des données libres et de longueur variable.
Avec un tel message, il est tout à fait possible d'imaginer que le champ Data de la trame du message ICMP soit utilisé pour transporter des données applicatives. Il serait ainsi possible d'imaginer un protocole complexe reposant sur des trames d'apparences anodines. Après tout, qui regarde le contenu du champ data des trames ICMP ?
Pour que ce protocole fonctionne, il suffit que la machine A puisse faire un ping de la machine B et que la machine B puisse faire un ping de la machine A.
Ce protocole fictif, mais réalisable est ni plus ni moins que de la stéganographie.
IV-D. Conclusion▲
En conclusion, il faut retenir que la stéganographie est une méthode de cryptographie faible : elle repose uniquement sur le fait que personne ne remarquera le canal caché. Dès lors que ce canal est connu, il n'y a plus aucune protection.
V. La cryptographie moderne▲
La cryptographie moderne repose maintenant uniquement sur les mathématiques. De plus, les règles de base sont :
- l'algorithme utilisé n'est pas secret. Il peut être diffusé librement, cela ne doit avoir aucun impact sur la facilité ou non à déchiffrer le message ;
- la clé de chiffrage utilisée est secrète.
Un protocole cryptographique bas√© sur la non-divulgation de l'algorithme math√©matique utilis√© n'est pas fiable. T√īt ou tard, l'algorithme utilis√© sera connu et le protocole deviendra faible. Au contraire, diffuser l'algorithme math√©matique utilis√© permet √† la communaut√© de valider et de tester la robustesse de cet algorithme.
V-A. Buts de la cryptographie▲
Globalement, la cryptographie permet de résoudre quatre problèmes différents :
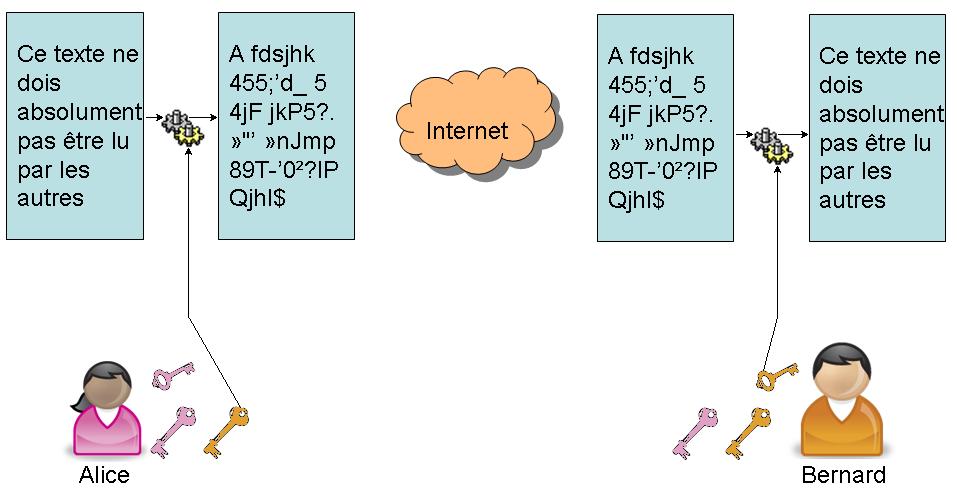
- la confidentialité. Le texte chiffré ne doit être lisible que par les destinataires légitimes. Il ne doit pas pouvoir être lu par un intrus ;
- l'authentification. Le destinataire d'un message doit pouvoir s'assurer de son origine. Un intrus ne doit pas être capable de se faire passer pour quelqu'un d'autre ;
- l'intégrité. Le destinataire d'un message doit pouvoir vérifier que celui-ci n'a pas été modifié en chemin. Un intrus ne doit pas être capable de faire passer un faux message pour légitime ;
- la non-répudiation. Un expéditeur ne doit pas pouvoir, par la suite, nier à tort avoir envoyé un message.
Il ne faut pas confondre cryptographie et codage. En effet, la cryptographie va s'attacher à cacher le sens d'un texte ; Le codage quant à lui s'attache à modifier le texte de façon à utiliser un support particulier. Par exemple, il existe le code Morse qui transforme les chiffres et lettres d'un texte en une succession de traits et de points afin de pouvoir utiliser le support télégraphique. Il existe aussi le code ASCII qui transforme les caractères en valeurs codées sur 8 bits (de 0 à 255) pour utiliser les supports informatiques. Il n'y a strictement rien de secret dans un codage.
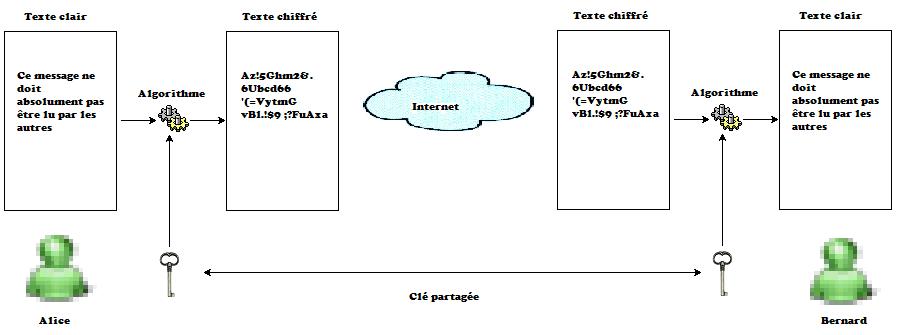
V-B. Alice, Bernard et les autres▲
Traditionnellement, pour illustrer les protocoles, on parle de communication entre des personnes fictives. Pour la cryptographie, par convention, ces personnes sont :
|
Français |
Anglais |
R√īle |
|---|---|---|
|
Alice |
Alice |
Alice veut envoyer un message à Bernard |
|
Bernard |
Bernard |
Bernard communique avec Alice |
|
Christine |
Carol |
S'il faut une 3e personne pour communiquer avec Alice et Bernard, c'est Christine. |
|
David |
Dave |
S'il faut une 4e personne pour communiquer avec Alice, Bernard et Christine, c'est David. |
|
Estelle |
Eve |
Estelle est une espionne qui peut écouter les communications entre Alice et Bernard. |
|
Martin |
Mallory |
Martin est un attaquant actif. Au contraire d'Estelle, il peut modifier les messages qu'il écoute, rejouer d'anciens messages, substituer ses propres messages, etc. |
Il existe encore d'autres pr√©noms utilis√©s¬†: Oscar, Trudy, Ivan, Gatien, Isaac, Nestor, etc. avec chacun un r√īle identifi√© dans un protocole cryptographique.
Ces noms ont été utilisés pour la première fois par Ronald Rivest dans son article de 1978 dans lequel il présentait les principes de l'algorithme RSA.
V-C. Quelques nombres pour fixer les id√©es▲
Comme on le verra plus loin, les méthodes cryptographiques utilisent des très grands nombres. Il est utile de comparer ces nombres par rapport à quelques mesures physiques de tous les jours. Attention toutefois, les nombres fournis dans le tableau suivant sont des approximations ou des valeurs couramment admises dans l'état actuel de nos connaissances.
|
Nombre de secondes dans un jour |
86 400 secondes |
|
Nombre de secondes dans une année |
31 536 000 secondes |
|
Nombre de secondes écoulées depuis la création de l'univers (13,7 milliards d'années) |
432 043 200 000 000 000 secondes ou 432 * 10^15 secondes |
|
Durée de vie d'un proton |
10^30 ann√©es soient 10^20 fois l'√Ęge de l'univers |
|
Masse du soleil |
2 * 10^33 grammes |
|
Nombre d'atomes dans un gramme de matière |
0,5 * 10^24 atomes |
|
Nombre d'atomes dans l'univers |
10^80 atomes |
Le but de ces quelques nombres est de montrer l'inutilit√© des attaques dites force brute. En effet, un cryptanalyste en herbe pourrait se dire ¬ę¬†Ce message est chiffr√© avec l'algorithme AES-256, il y a 2^256 cl√©s possibles (soient environ 10^76 cl√©s), testons-les toutes pour d√©chiffrer le message¬†¬Ľ. √Ä raison de 100 milliards de tentatives par seconde (ce qui est √©norme), il faudrait 10^58 secondes pour tester toutes les cl√©s. Ce temps de calcul n√©cessaire est beaucoup plus long que l'√Ęge de l'univers.
V-D. Les diff√©rents modes de chiffrement▲
Le mode de chiffrement correspond à la manière dont on va utiliser un algorithme de chiffrement donné. Ce mode de chiffrement consiste par exemple à rajouter de la contre-réaction entre l'entrée et la sortie de l'algorithme afin de lui rajouter des caractéristiques bien précises. Les différentes mode de chiffrement utilisés sont les suivants :
- Le mode ECB pour Electronic Code Book
- Le mode CBC pour Cipher Block Chaining
- Le mode chiffrement en continu
- Le mode CTAK pour Cipher Text Auto Key
- Le mode CFB pour Cipher Feed Back
- Le mode KAK pour Key Auto Key
- Le mode OFB pour Output Feed Back
- Le mode CTR pour CounTeR
- Le mode BC pour Block Chaining
- Le mode PCBC pour Propagating Cipher Block Chaining
- Le mode CBCC pour Cipher Block Chaining with Checksum
- Le mode OFBNLF pour Output Feed Back mode with a Non Linear Function
- Le mode PBC pour Plaintext Block Chaining
- Le mode PFB pour Plaintext Feed Back
- Le mode CBCPD pour Cipher Block Chaining of Plaintext Difference
- Le mode CTS pour Cipher Text Stealing
Dans les paragraphes suivants, nous allons regarder un peu plus en détail les modes ECB, CBC, CFB et OFB. Les autres modes sont nommés à des fins d'exhaustivité, mais sont rarement utilisés.
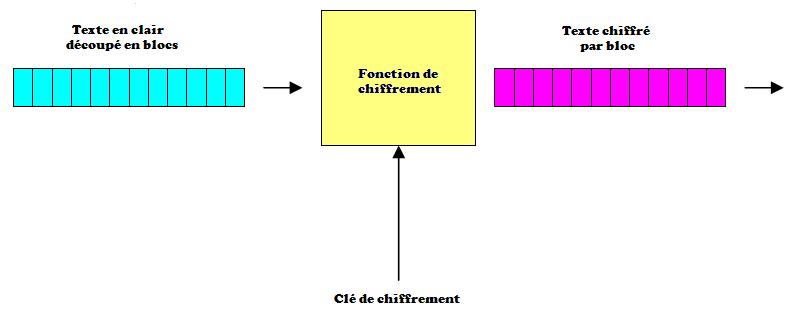
V-D-1. Le mode ECB▲
Ce mode est le plus simple : un même bloc est toujours codé de la même manière. Il n'y a pas de rétroaction de l'entrée ou de la sortie sur la fonction de chiffrement.
Les avantages de ce mode sont les suivants :
- Le travail de chiffrement ou de déchiffrement peut être parallélisé. Plusieurs machines ou CPU peuvent travailler simultanément sur des parties différentes du message.
- Il permet un accès aléatoire dans le texte chiffré.
- Une erreur de transmission d'un bit affecte uniquement le décodage du bloc courant.
Par contre, ce mode a les désavantages suivants :
- Les répétitions du texte en clair ne sont pas masquées et se retrouvent sous la forme de répétitions de textes chiffrés.
- Des portions complètes du message peuvent être modifiées, répétées ou remplacées sans difficulté.
- La perte de synchronisation (perte ou ajout d'un bit) est irrécupérable.
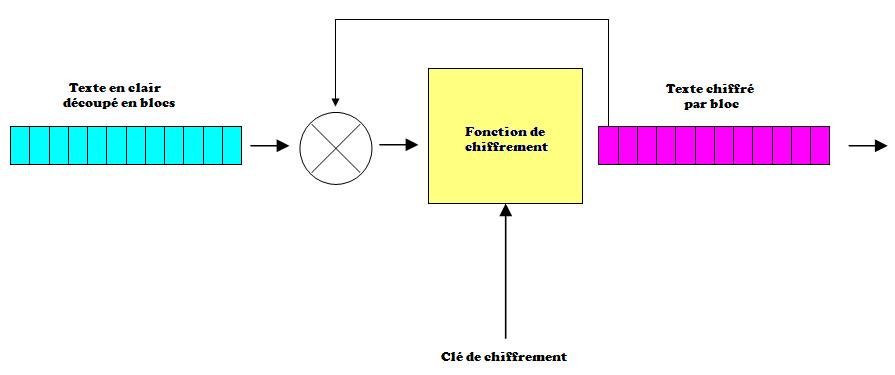
V-D-2. Le mode CBC▲
Dans ce mode de chiffrement, chaque bloc de texte en clair est d'abord combiné par un ou exclusif avec le dernier bloc du texte chiffré. La sortie de ce ou exclusif est ensuite appliquée à la fonction de chiffrement.
Ce mode de chiffrement dispose en plus d'un vecteur d'initialisation appelée IV (pour Initialisation Vector) qui permet d'initialiser le processus quand aucun bloc n'a encore été chiffré.
Les avantages de ce mode sont les suivants :
- les répétitions de texte en clair sont masquées dans le texte chiffré ;
- la valeur du vecteur d'initialisation IV n'a pas besoin d'être secrète.
Par contre, ce mode a les désavantages suivants :
- deux textes en clair commençant pareil auront le même début de texte chiffré ;
- une erreur de transmission d'un bit affecte uniquement le décodage du bloc courant ainsi que le décodage du même bit dans le bloc suivant ;
- la perte de synchronisation (perte ou ajout d'un bit) est irrécupérable.
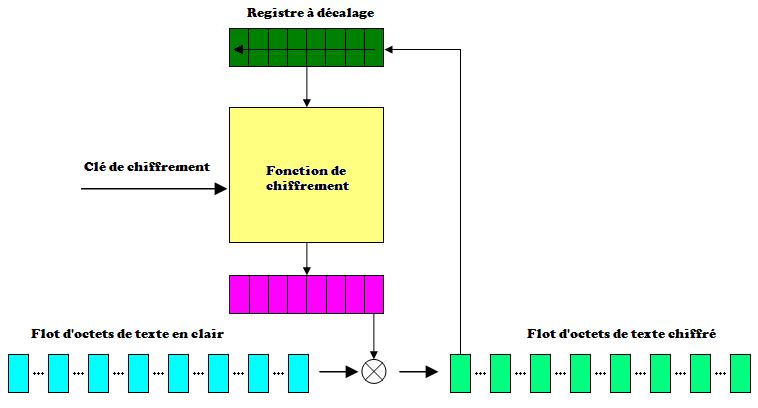
V-D-3. Le mode CFB▲
Les modes ECB et CBC travaillent avec sur des blocs de texte en clair (64 bits par exemple). Ces modes ne sont pas utilisables lorsque le chiffrement ne peut débuter que lorsqu'un bloc est complet. Sur des applications réseau, cela peut poser des problèmes, car les valeurs à chiffrer arrivent de manière asynchrone sous forme d'octets et doivent être transmises immédiatement (cas du protocole telnet par exemple).
Le registre à décalage est initialisé avec un vecteur d'initialisation. Le bloc complet est alors chiffré. L'octet de poids faible du texte chiffré est combiné par un ou exclusif avec l'octet de texte en clair. Le résultat de cette opération est alors transmis en même temps qu'il est injecté dans le registre à décalage.
Les avantages de ce mode sont les suivants :
- il est possible de chiffrer un flot de valeurs plus petites que la taille standard du bloc géré par l'algorithme ;
- les répétitions de texte en clair sont masquées dans le texte chiffré ;
- la valeur du vecteur d'initialisation IV n'a pas besoin d'être secrète ;
- la perte de synchronisation (perte ou ajout d'un bit) est récupérable.
Par contre, ce mode a les désavantages suivants :
- une erreur de transmission d'un bit affecte uniquement le décodage du bloc courant ainsi que le décodage du même bit dans le bloc suivant.
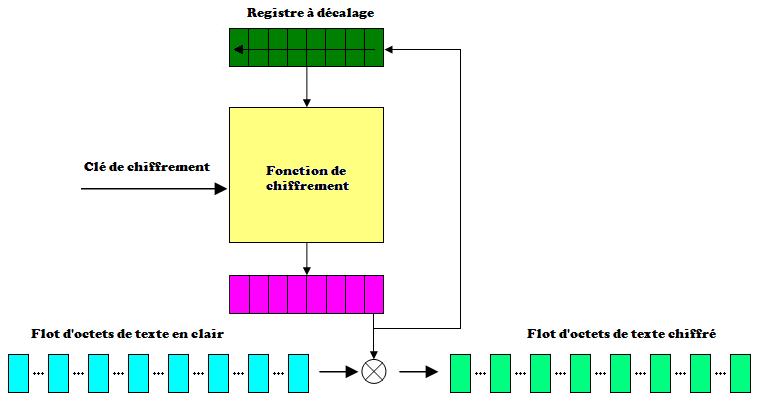
V-D-4. Le mode OFB▲
Le mode OFB ressemble au mode CFB. La seule différence est que l'octet injecté dans le registre à décalage est l'octet de poids faible du texte chiffré.
Les avantages de ce mode sont les suivants :
- les répétitions de texte en clair sont masquées dans le texte chiffré ;
- la valeur du vecteur d'initialisation IV n'a pas besoin d'être secrète ;
- ce mode n'amplifie pas les erreurs. Une erreur de transmission d'un bit affecte uniquement ce bit lors du décodage.
Par contre, ce mode a les désavantages suivants :
- la perte de synchronisation (perte ou ajout d'un bit) est irrécupérable.
V-E. Quel mode choisir¬†?▲
Les quatre modes présentés ainsi que tous les autres ont chacun leurs avantages et leurs faiblesses. Il conviendra de choisir le mode en fonction de ce que l'on veut faire.
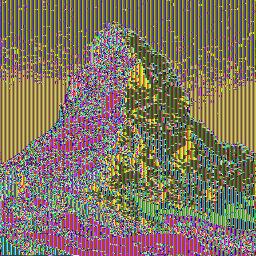
Pour finir, voici trois photos du mont Cervin dans les Alpes (source Wikipédia). La première photo est le texte en clair, la seconde est le texte chiffré de la photo utilisant un algorithme en mode ECB et enfin la dernière photo utilise le même algorithme en mode CBC.
|
Non chiffré |
Chiffré en mode ECB |
Chiffré en mode CBC |
|---|---|---|
|
|
|
|
Ces photos montrent clairement que le mode ECB n'est pas adapté au chiffrement de photographies. Ceci ne veut toutefois pas dire que le mode ECB ne doit pas être utilisé, il a d'autres domaines d'utilisation.
Après le parcours des différents modes de chiffrement utilisables, nous allons maintenant nous intéresser aux différents algorithmes de chiffrement. Il existe en tout quatre grandes familles d'algorithmes utilisées par la cryptographie. Ces familles sont :
- les algorithmes de calcul d'empreinte ;
- les algorithmes symétriques ;
- les algorithmes asymétriques ;
- les méthodes de génération de nombres aléatoires.
Chacune de ces familles est présentée dans les paragraphes suivants.
VI. Les algorithmes de calcul d'empreinte▲
Un algorithme de calcul d'empreinte est un algorithme qui transforme un texte en clair en un nombre (une empreinte numérique) qui soit représentatif de ce texte en clair. Le but de ces algorithmes est qu'une altération aussi minime soit elle du texte en clair puisse être détectée par le fait que la nouvelle empreinte est différente et même très différente de la précédente. On parle aussi de fonction de hachage.
En général, ce type d'algorithme fournit comme résultat un nombre dont la taille est fixe et ce quelle que soit la taille du texte en clair en entrée.
Pour ce type d'algorithme, on parlera aussi de la notion de collision. Une collision de texte en clair est le fait que deux textes en clair différents provoquent la même empreinte.
Les caractéristiques d'un algorithme d'empreinte utilisé en cryptographie sont les suivantes :
- difficulté à retrouver le texte en clair à partir de l'empreinte ;
- difficulté à trouver un second texte en clair qui donne la même empreinte numérique qu'un autre texte en clair donné ;
- difficulté à trouver deux textes en clair qui donnent la même empreinte numérique.
Il est évident que plus le nombre de collisions est faible, et donc plus le nombre généré en sortie est large, plus l'algorithme est fiable, mais ce n'est pas le seul critère de fiabilité. Il faut aussi qu'il soit dur de générer des textes en clair différents pour une empreinte numérique donnée et il faut aussi que la plus petite variation dans le texte en clair se traduise par une grande variation dans l'empreinte générée.
Bien que les algorithmes checksum et CRC ne soient pas des algorithmes forts au sens cryptographique du terme, il m'a semblé intéressant de les faire figurer dans ce paragraphe pour des raisons historiques et aussi parce que leurs concepts sont ceux d'une fonction de calcul d'empreinte. Ces deux algorithmes ne sont pas suffisamment forts pour la cryptographie, car le nombre d'empreintes possibles est vraiment trop petit (2^16 pour l'algorithme CHECKSUM ou 2^32 pour l'algorithme CRC-32 à comparer au 2^128 du MD5 ou même 2^160 du SHA-1).
Ce paragraphe s'intéressera ensuite aux deux familles principales d'algorithme de calcul d'empreinte utilisées en cryptographie : la famille des MD et la famille des SHA.
VI-A. CHECKSUM▲
La fonction de checksum peut √™tre consid√©r√©e comme une fonction de calcul d'empreinte. Son but est de v√©rifier qu'il n'y a pas d'erreur de transmission. En g√©n√©ral, les fonctions de checksum sont plut√īt utilis√©es dans les communications, mais pas en cryptographie, car la taille du nombre g√©n√©r√© n'est pas suffisamment grande pour √™tre qualifi√©e de fiable math√©matiquement parlant.
On retrouve par exemple ce type d'algorithme dans l'en-tête des paquets IP.
En-tête IP tel que défini par le RFC 791
0 1 2 3
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
|Version| Taille|Type de Service| longueur totale |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Identification |Flags| Fragment Offset |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Durée de vie | Protocole | Checksum d'en-tête |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Adresse Source |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Adresse Destination |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| Options | Bourrage |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+Dans l'en-t√™te du paquet IP, on retrouve un champ nomm√© checksum d'en-t√™te qui est la somme de contr√īle de l'en-t√™te. Si par hasard, un bit de l'en-t√™te venait √† √™tre modifi√© au cours du transfert, cette modification serait probablement d√©tect√©e par le contr√īle du checksum d'en-t√™te et le paquet serait ignor√©.
L'algorithme utilisé est le suivant.
- Il s'agit du complément à un sur 16 bits de la somme des compléments à un de tous les octets de l'en-tête pris par paires (mots de 16 bits). Lorsque l'on calcule le checksum, la valeur du checksum de l'en-tête calculé est initialisée à 0.
- Lorsqu'un des champs de l'en-tête IP est modifié (le champ TTL par exemple lorsqu'il est décrémenté par un routeur), ce checksum est recalculé.
Cet algorithme, bien qu'élémentaire et rudimentaire, a montré son efficacité dans le cadre de cette utilisation.
VI-B. CRC▲
L'acronyme CRC provient de l'anglais Cyclic Redundancy Check ou encore en fran√ßais, Contr√īle de Redondance Cyclique.
En fait, le CRC est le reste de la division enti√®re d'un nombre par un polyn√īme. Ce polyn√īme poss√®de des caract√©ristiques math√©matiques particuli√®res.
Le but du CRC est de d√©tecter une erreur de transmission et dans certains cas seulement, de corriger cette erreur de transmission (si l'erreur ne porte pas sur trop de bits bien s√Ľr).
Une trame Ethernet est termin√©e par un CRC qui permet de d√©tecter une erreur de transmission, le polyn√īme utilis√© est un des nombreux CRC 32 existants appel√© aussi CRC-32-IEEE 802.3 dont la formule est la suivante¬†:
- x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x^1 + 1
Un autre CRC est utilisé par exemple dans le cadre des protocoles X25 ou HDLC ou PPP, il s'agit d'un des CRC 16 nommé CRC-16-CCITT dont la formule est la suivante :
- x^16 + x^12 + x^5 + 1
La particularité de ce type d'algorithme est qu'il permet parfois de réparer une erreur de transmission par contre, ce type d'algorithme n'a pas sa place en cryptographie.
On se reportera à l'excellent tutoriel sur le calcul des CRC écrit par DVSoft.
VI-C. L'algorithme MD5▲
Les algorithmes MD2, MD4 et MD5 sont des algorithmes de calcul d'empreinte numérique inventés par Ronald Rivest. Le mot MD signifie Message Digest.
Le résultat généré est un nombre sur 128 bits (16 octets) à partir de messages de 512 bits (64 octets).
MD2 est la première version de cet algorithme inventée en 1989. Il a ensuite été supplanté par l'algorithme MD4. Finalement, l'algorithme MD4 a été abandonné suite à des faiblesses de conception mises en évidence par des attaques.
MD5 est l'évolution de MD4 faite par Ronald Rivest en 1991 afin de pallier les faiblesses identifiées. Cet algorithme est entièrement décrit dans la RFC 1321. Cette RFC comprend entre autres une implémentation de l'algorithme en C qui est directement compilable.
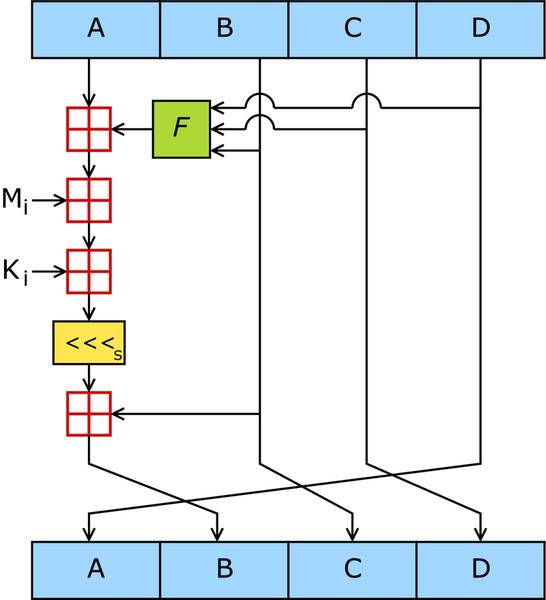
MD5 comprend 64 blocs de ce type, groupés en quatre tours de 16 opérations. F est une fonction non linéaire, qui varie selon le tour. Mi symbolise un bloc de 32 bits provenant du message à hacher et Ki est une constante de 32 bits, différentes pour chaque opération.
Au jour d'aujourd'hui, cet algorithme n'est plus considéré comme fiable et devrait être abandonné suite aux différentes attaques menées avec succès depuis 2004.
VI-D. L'algorithme SHA-1▲
Le SHA-0 est l'ancêtre des algorithmes SHA-1 et successeurs. Il a été inventé en 1993 et il a été rapidement abandonné pour des raisons de sécurité insuffisante. Il était soupçonné de contenir des faiblesses qui permettraient d'aboutir rapidement à des collisions. Le mot SHA signifie Secure Hash Algorithm.
Le SHA-0 a été modifié pour devenir le SHA-1 en 1995. Le résultat généré est un nombre sur 160 bits (20 octets) à partir de messages de 512 bits (64 octets).
Pour chaque bloc l'algorithme calcule 80 tours successifs et applique une s√©rie de transformations sur l'entr√©e. La premi√®re √©tape consiste √† calculer 80 valeurs sur 32 bits. Les 16 premi√®res valeurs sont obtenues directement √† partir du bloc en entr√©e. Les 64 autres sont calcul√©es successivement. Le SHA-1 les obtient gr√Ęce √† une rotation (absente dans SHA-0) qui est appliqu√©e sur le r√©sultat d'un XOR. Il utilise pour cela 4 mots obtenus dans les it√©rations pr√©c√©dentes. On d√©finit ensuite 5 variables qui sont initialis√©es avec des constantes (sp√©cifi√©es par le standard). Le SHA-1 utilise encore 4 autres constantes dans ses calculs. Si un bloc de 512 bits a d√©j√† √©t√© calcul√© auparavant, les variables sont initialis√©es avec les valeurs obtenues √† la fin du calcul sur le bloc pr√©c√©dent.
D'autres versions de cet algorithme (SHA-256, SHA-384 et SHA-512) existent aussi. Elles offrent respectivement des empreintes numériques de 256, 384 et 512 bits (soient 32, 48 et 64 octets).
VI-E. D'autres algorithmes▲
Il existe encore d'autres algorithmes de calcul d'empreintes parmi lesquels, on peut citer :
- Boognish
- Construction de Davies-Meyer
- Construction de Matyas-Meyer-Oseas
- Construction de Merkle-Damgård
- Construction de Miyaguchi-Preneel
- FFT-hash
- HAS-160
- Haval
- LM hash
- N-hash
- PANAMA
- RIPEMD, RIPEMD-128, RIPEMD-160, RIPEMD-256
- Snefru
- StepRightUp
- Tiger
- VSH
- Whirlpool
VII. Les algorithmes sym√©triques▲
Un algorithme symétrique est un algorithme qui permet de transformer un texte en clair en texte chiffré en utilisant une clé et de retransformer le texte chiffré en texte en clair en utilisant la même clé.
Le secret de la communication est uniquement assuré par la clé qui est utilisée lors de la phase de chiffrement et de déchiffrement. L'algorithme utilisé ne fait pas partie du secret.
On parle d'algorithmes symétriques, car c'est la même clé qui sert à la fois au chiffrement et au déchiffrement du message.
Dans ce paragraphe nous allons plus particulièrement nous intéresser aux algorithmes DES, AES et IDEA.
VII-A. L'algorithme DES▲
L'algorithme DES (Data Encryption Standard) est né dans les années 1970 sous l'impulsion du National Bureau of Standards américain. Celui-ci voulait promouvoir un système de chiffrement qui permettrait à différents interlocuteurs de communiquer en toute sécurité tout en utilisant un algorithme fiable et commun.
L'algorithme Lucifer est l'algorithme, conçu par IBM, qui fut retenu. La NSA (National Security Agency) imposa toutefois quelques modifications dans l'algorithme. Ces modifications imposées furent les causes de beaucoup de rumeurs.
L'algorithme DES fut officiellement adopté le 23 novembre 1976, il est décrit dans le document FIPS PUB 46 modifié depuis par le FIPS PUB 46-3.
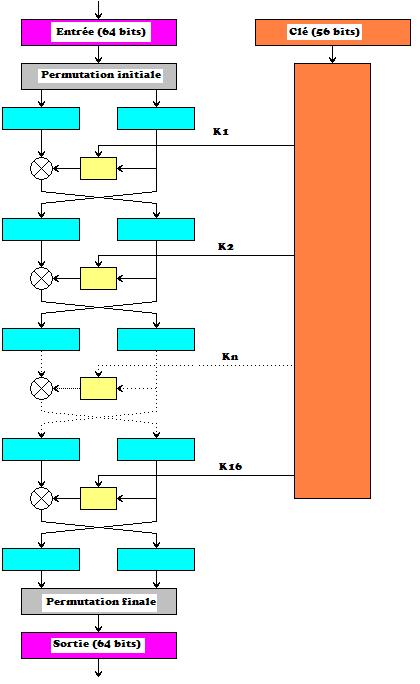
L'algorithme DES est un algorithme symétrique de chiffrement par bloc de 64 bits (soient 8 octets) fonctionnant avec une clé de 56 bits. Il fonctionne sur 16 rondes et lors de chacune des rondes, le bloc de 64 bits est découpé en 2 blocs de 32 bits.
Le bloc de droite qui subit les transformations à l'aide d'une des clés de 48 bits dérivées de la clé principale de 56 bits.
Les 32 bits de droite sont d'abord √©tendus √† 48 bits √† l'aide d'une op√©ration particuli√®re. Ensuite, une op√©ration de ou exclusif est effectu√©e entre ces 48 bits et les 48 bits d'une des cl√©s d√©riv√©es de la cl√© principale. Et enfin, les 48 bits du r√©sultat sont ensuite condens√©s sur 32 bits √† l'aide des bo√ģtes S1 √† S8. Ces huit bo√ģtes ont √©t√© impos√©es par la NSA et ont √©t√© la cause de toutes les rumeurs concernant cet algorithme. Chacune de ces bo√ģtes transforme 6 bits en 4 bits selon un sch√©ma encore une fois tr√®s particulier.
Comme on peut le voir, cet algorithme n'est pas très facile à transformer en programme compte tenu de toutes les permutations et compressions de bits. Par contre, c'est un algorithme très facile à implémenter en électronique. Il ne faut pas oublier qu'en 1970 on faisait plus de choses plus vite en électronique qu'en informatique.
Beaucoup d'applications encore de nos jours utilisent le DES. C'est par exemple l'algorithme qui a été utilisé pendant très longtemps (et encore maintenant pour certains) sur les ordinateurs de type Unix pour chiffrer les mots de passe des utilisateurs.
Cet algorithme ne devrait maintenant plus être utilisé du fait de son petit nombre de clés (2^56) qui paraissait énorme en 1970, mais qui est maintenant petit comparé à d'autres algorithmes et à la puissance de calcul disponible (le calcul distribué permet maintenant de trouver une clé en 24 heures). De plus, de nombreuses attaques cryptographiques ont permis de découvrir des petites faiblesses dans le DES.
Il faut noter aussi que le DES possède 4 clés faibles et 12 clés semi-faibles. La probabilité (relativement faible) de tomber sur une de ces clés est de .
VII-B. L'algorithme 3-DES▲
L'algorithme 3-DES utilise l'algorithme DES avec 2 ou 3 clés différentes. L'algorithme va d'abord chiffrer avec une clé, déchiffrer avec la deuxième clé est enfin chiffrer encore avec la troisième clé.
Que l'on utilise cet algorithme avec 2 clés différentes (112 bits) ou 3 clés différentes (168 bits), la clé effective est de 112 bits.
Pour les mêmes raisons, le double DES n'existe pas, car la clé effective n'est que de 57 bits soit 1 bit de plus que le simple DES.
VII-C. L'algorithme AES▲
De même qu'en 1970 pour le DES avec le National Bureau of Standards américain, l'algorithme AES est issu d'un appel d'offres lancé par le NIST américain (National Institute of Standards and Technology) en 1997.
C'est l'algorithme Rijndael dont les deux concepteurs sont Joan Daemen et Vincent Rijmen qui est choisi comme nouveau standard pour remplacer le DES vieillissant.
L'algorithme AES est un algorithme symétrique de chiffrement par bloc de 128 bits (soient 16 octets) fonctionnant avec une clé de 128, 192 ou 256 bits.
VII-D. L'algorithme IDEA▲
IDEA pour International Data Encryption Algorithm est un algorithme de chiffrement conçu par Xuejia Lai et James Massey et présenté pour la première fois en 1991.
L'algorithme IDEA est un algorithme symétrique de chiffrement par bloc de 64 bits (soient 8 octets) fonctionnant avec une clé de 128 bits.
La particularité de cet algorithme est que les opérations qu'il utilise en interne s'adaptent très facilement à une programmation informatique sur machine de 16 bits.
VII-E. L'algorithme du masque jetable▲
L'algorithme du masque jetable consiste à utiliser un flux de nombres aléatoires qui va être combiné par une opération ou exclusif sur le texte en clair pour générer le texte chiffré.
Les contraintes imposées par ce système sont :
- le flux aléatoire doit être vraiment aléatoire (voir le chapitre au sujet de la génération de nombres aléatoires) ;
- le destinataire du message doit recevoir par un moyen fiable une copie du flux aléatoire utilisé pour chiffrer le texte en clair (CD-ROM convoyé par porteur spécial, etc.) ;
- un flux aléatoire déjà utilisé ne doit jamais être réutilisé.
Si ces contraintes sont parfaitement respectées, le texte chiffré est indéchiffrable et inattaquable pour quiconque ne possède pas une copie du flux aléatoire.
VII-F. D'autres algorithmes▲
Il existe encore d'autres algorithmes symétriques parmi lesquels on peut citer :
- Blowfish
- Fox
- Frog
- Misty1
- MMB
- 3-Way
- RC2, RC4, RC5
- REDOC
- SHACAL
VIII. Les algorithmes asym√©triques▲
Les algorithmes sym√©triques vus dans le chapitre pr√©c√©dent sont tous fiables, mais ils posent un probl√®me, c'est celui de l'√©change de la cl√©¬†: comment transmettre de mani√®re fiable √† mon interlocuteur la cl√© de chiffrement utilis√©e pour chiffrer le message que je lui envoie¬†? Il y a bien s√Ľr le t√©l√©phone, mais il y a aussi les √©coutes t√©l√©phoniques.
Les algorithmes asymétriques ont été inventés pour pallier précisément le problème de transmission sécurisée de la clé.
On parle d'algorithmes asymétriques, car ce n'est pas la même clé qui sert au chiffrement et au déchiffrement. Dans le cas de ces algorithmes, on parlera alors de clé privée et de clé publique. Ces deux clés, clé privée et clé publique, sont intimement liées par une fonction mathématique complexe.
Les algorithmes asymétriques possèdent deux modes de fonctionnement.
- Le mode chiffrement dans lequel l'√©metteur chiffre un fichier avec la cl√© publique du destinataire pour chiffrer. Le destinataire utilise sa cl√© priv√©e pour d√©chiffrer le fichier. Dans ce mode, l'√©metteur est s√Ľr que seul le destinataire peut d√©chiffrer le fichier.
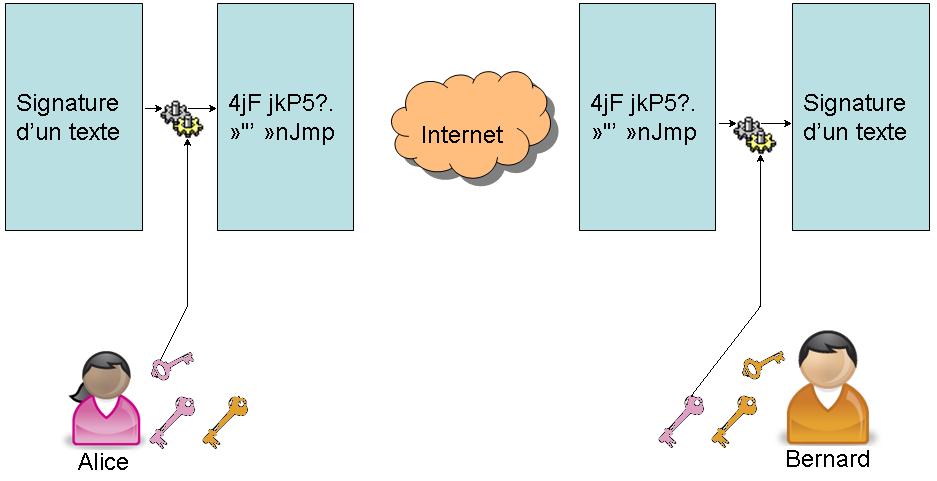
- Le mode signature dans lequel l'√©metteur signe un fichier avec sa propre cl√© priv√©e. Le destinataire utilise la cl√© publique de l'√©metteur pour v√©rifier la signature du fichier. Dans ce mode, le destinataire est s√Ľr que c'est bien l'√©metteur qui a envoy√© le fichier.
Donc pour résumer :
- l'émetteur chiffre avec la clé publique du destinataire, le destinataire déchiffre avec sa clé privée ;
- l'émetteur signe avec sa clé privée, le destinataire vérifie la signature avec la clé publique de l'émetteur.
VIII-A. L'algorithme DH▲
Whitfield Diffie et Martin Hellman ont travaillé ensemble en 1974 sur ce problème. Comment deux personnes sur Internet peuvent-elles communiquer de manière sécurisée et donc pour cela s'échanger de manière fiable et sécurisée une clé de chiffrement permettant l'usage d'un des protocoles symétriques.
Ils ont tourn√© leurs recherches vers les fonctions non r√©versibles, c'est-√†-dire les fonctions de la forme y = f(x) o√Ļ quand on conna√ģt x, il est tr√®s facile de calculer y, mais quand on conna√ģt y, il est impossible de recalculer x.
Par exemple, la fonction y = x * x est une fonction réversible. Connaissant x, il est facile de calculer y et connaissant y, il est facile de calculer x. La fonction réversible de y = x * x est x = racine(y).
Les fonctions qu'ils ont utilisées sont les fonctions de l'arithmétique modulo, car elles ne sont pas réversibles.
Par exemple y = x (modulo 7) n'est pas une fonction réversible. En effet, pour x = 11, on obtient y = 4 mais pour y = 4, on obtient x = 11 ou x = 18 ou encore x = 25 et une infinité d'autres solutions encore.
Finalement, en 1976, ils découvrirent une fonction du type y = Y^x (modulo P) qui permet cet échange sécurisé.
Un exemple d'un échange sécurisé de clé est schématisé dans le tableau suivant. Alice veut communiquer avec Bernard et Estelle peut écouter les échanges.
|
Alice |
Estelle |
Bernard |
|---|---|---|
|
Nous utiliserons la fonction y = 11^x modulo 13 |
Ha ! Ils vont utiliser la fonction y = 11^x modulo 13 |
OK, utilisons la fonction y = 11^x modulo 13 |
|
Alice choisit un nombre secret A = 5 |
Estelle ne sait pas les nombres secrets A et B choisis par Alice et Bernard. |
Bernard choisit un nombre secret B = 8 |
|
Alice calcule le nombre A' = 11^A modulo 13. À' = 7 et envoie ce nombre A' = 7 à Bernard de manière quelconque |
Ha ha ! Le nombre A' d'Alice est 7 et le nombre B' de Bernard est 9 |
Bernard calcule son nombre B' = 11^B modulo 13. B' = 9 et envoie ce nombre B' = 9 de manière quelconque à Alice |
|
Alice prend le nombre B' = 9 de Bernard et calcule le résultat de : B'^A modulo 13 et obtient : 3 |
Estelle ne sait pas calculer ces nombres, car elle ne dispose ni du nombre secret initial d'Alice A, ni du nombre secret initial de Bernard B. |
Bernard prend le nombre A' = 7 d'Alice et calcule le résultat de : À'^B modulo 13 et obtient : 3 |
En final, Alice et Bernard obtiennent un même nombre secret 3 qu'ils peuvent utiliser comme clé pour un algorithme symétrique choisi. Le calcul de cette clé s'est effectué en s'échangeant deux valeurs presque quelconques. Estelle, qui pourtant a la possibilité d'écouter les échanges, ne sait rien de cette clé et n'a pas la possibilité de la calculer.
Bien s√Ľr, dans la pratique, les nombres choisis seront plus grands, mais le principe reste le m√™me.
Avec cet algorithme, Whitfield Diffie et Martin Hellman ont prouvé que l'échange des clés de manière fiable et sécurisée était possible sans avoir besoin de se rencontrer.
Cet algorithme, bien que simple souffre d'un défaut. Il faut que Alice et Bernard se synchronisent afin de pouvoir s'échanger un minimum d'information : les paramètres de la fonction utilisée ainsi que les valeurs A' et B'. Cela signifie qu'Alice doit attendre que Bernard soit réveillé pour lui envoyer un message.
L'échange sécurisé des clés étant réglé, il restait le problème de synchronisation obligatoire à supprimer.
VIII-B. L'algorithme RSA▲
Suite aux travaux réalisés par Whitfield Diffie et Martin Hellman, Ronald Rivest, Adi Shamir et Leonard Adleman ont eux aussi travaillé tous les trois sur les algorithmes asymétriques à partir de 1975.
L'algorithme qu'ils ont mis au point repose aussi sur une fonction a sens unique ou plut√īt une fonction tr√®s difficilement r√©versible. Cette fonction difficilement r√©versible est la factorisation d'un nombre en produit de facteurs premiers. En effet, autant, il est tr√®s facile de choisir deux nombres (48 et 52 par exemple) et de calculer leur produit (2496), autant il est long et p√©nible d'extraire les facteurs premiers du nombre 2397 qui sont 47 et 51.
Le principe de l'algorithme RSA est donc basé sur la difficulté de factoriser un nombre surtout quand ce nombre est très grand et qu'il est le produit de deux nombres premiers très grands eux aussi.
L'algorithme imaginé est le suivant.
- Alice choisit au hasard deux nombres premiers p et q (13 et 17 par exemple).
- Elle construit le produit de ces deux nombres N (221 dans notre exemple).
- Elle choisit un nombre e. Ce nombre ne doit pas être un diviseur de (p-1) * (q-1) (5 par exemple).
- La clé publique d'Alice est composée de la paire de nombre e et N (5 et 221 dans notre exemple). Cette clé publique peut être publiée dans un annuaire.
- Alice calcule ensuite le nombre d donné par la formule e * d = 1 modulo ((p-1) * (q-1)) (77 dans notre exemple). Ce nombre représente la clé privée d'Alice.
- Bernard veut envoyer le message bonjour à Alice. Pour cela, il convertit le mot en valeurs (nous prendrons les valeurs issues du code ASCII dans notre exemple). La conversion donne les valeurs 98, 111, 110, 106, 111, 117, 114.
- La formule utilisée pour chiffrer les valeurs est la suivante :
dans lequel ci représente la valeur chiffrée de mi, e et N représentants les paramètres publics de la clé d'Alice.
- Avec le texte en clair 98, 111, 110, 106, 111, 117, 114, et en appliquant la formule pour chacune des valeurs on obtient le texte chiffré suivant : 115, 76, 145, 123, 76, 104, 173.
- Pour déchiffrer le message, Alice utilise la formule suivante :
dans lequel mi représente la valeur en clair de ci, d et N représentants les paramètres publics et privés de la clé d'Alice.
- Avec le texte chiffré 115, 76, 145, 123, 76, 104, 173, et en appliquant la formule pour chacune des valeurs on obtient à nouveau le texte en clair d'origine : 98, 111, 110, 106, 111, 117, 114.
Cet exemple montre que les param√®tres publics e et N suffisent √† chiffrer un message et que les param√®tres priv√©s et publics d et N suffisent pour d√©chiffrer le message. Bien s√Ľr, dans la pratique, les nombres choisis seront plus grands, mais le principe reste le m√™me.
Alice peut donc diffuser librement sa clé publique (les paramètres e et N). Toute personne qui veut communiquer avec Alice peut récupérer la clé publique d'Alice et lui envoyer un message chiffré. Alice est la seule à pouvoir déchiffrer ce message puisqu'elle est la seule à détenir le paramètre d de sa clé privée.
De plus Alice et Bernard n'ont plus besoin de se synchroniser pour commencer l'échange puisque la clé publique est disponible dans un annuaire public et que n'importe qui peut aller la chercher à tout moment pour l'utiliser.
La force de l'algorithme repose sur la difficulté à factoriser N. Si la factorisation était facile à réaliser, Estelle pourrait recalculer les nombres p et q et, connaissant e, elle pourrait alors calculer d et donc elle pourrait déchiffrer le message destiné à Alice.
La taille des clés RSA devrait aujourd'hui être au minimum de 1024 bits (309 chiffres décimaux). En effet, en mai 2005, le nombre RSA-200, un nombre de 663 bits (200 chiffres décimaux) a été factorisé. Ce nombre RSA-200 est le suivant :
RSA-200 =
27997833911221327870829467638722601621070446786955428537560009929326128400107609
34567105295536085606182235191095136578863710595448200657677509858055761357909873
4950144178863178946295187237869221823983
=
35324619344027701212726049781984643686711974001976250236493034687761212536794232
00058547956528088349
*
79258699544783330333470858414800596877379758573642199607343303414557678728181521
35381409304740185467Une autre utilisation de l'algorithme RSA concerne la signature. En effet, si Alice chiffre un document avec sa clé privée, tout le monde peut obtenir la clé publique d'Alice disponible dans un annuaire et déchiffre ce texte. Le fait de pouvoir déchiffrer le texte avec la clé publique d'Alice prouve que c'est bien Alice qui l'a chiffré puisqu'elle est la seule à posséder la clé privée.
Pour résumer :
- l'émetteur chiffre un message avec la clé publique du destinataire de façon à ce que seul le destinataire puisse déchiffrer le message avec sa clé privée ;
- l'émetteur signe un message avec sa clé privée de façon à ce que le destinataire puisse vérifier la signature du message avec la clé publique de l'émetteur.
VIII-C. D'autres algorithmes▲
Il existe encore d'autres algorithmes asymétriques parmi lesquels, on peut citer :
- Cryptographie sur les courbes elliptiques
- Cryptographie sur les courbes hyper elliptiques
- Crypto système de Blum-Goldwasser
- Crypto système de ElGamal
- Crypto système de Goldwasser-Micali
- Algorithme de Guillou-Quisquater
- Crypto système de McEliece
- Crypto système de Paillier
- Crypto système de Rabin
- Algorithme LLL
IX. Les m√©thodes de g√©n√©ration de nombres al√©atoires▲
On l'a vu dans les chapitres précédents, les algorithmes cryptographiques demandent souvent des nombres aléatoires. Ces nombres aléatoires peuvent être utilisés pour générer une clé aléatoire ou encore pour générer une clé publique et une clé privée pour l'algorithme RSA. Dans le cas de l'algorithme RSA, il faut en plus que ces nombres aléatoires soient premiers, mais il existe des algorithmes rapides pour déterminer la primalité d'un nombre.
Mais d'abord, quelles sont les caractéristiques d'une suite de nombres aléatoire ? Les mathématiciens aujourd'hui ne savent pas bien définir la notion d'aléatoire. Toutefois, on retient les caractéristiques suivantes.
- La répartition des nombres de la suite est équilibrée, c'est-à-dire que statistiquement, il y a autant de 0 que de 1.
- La suite de nombres ne possède pas de séquences plus ou moins longues de nombres qui se répètent.
Il existe plusieurs méthodes pour générer des nombres aléatoires.
- La m√©thode des d√©s ou le tirage √† pile ou face. On lance un d√© ou une pi√®ce et on rel√®ve la valeur sortie. Cette m√©thode ne g√©n√®re pas des nombres al√©atoires, mais plut√īt des nombres impr√©visibles. En effet, m√™me si l'on conna√ģt les conditions initiales (force du lancer, poids du d√©, hauteur de la table, etc.), il est impossible de conna√ģtre le r√©sultat, car cela rel√®ve de la th√©orie du chaos. Les ph√©nom√®nes chaotiques ne produisent pas des nombres al√©atoires, ils produisent des nombres chaotiques.
- Les g√©n√©rateurs de nombres pseudo al√©atoires. Il s'agit d'algorithmes qui g√©n√®rent des s√©quences de nombres qui ressemblent √† des nombres al√©atoires. Les nombres sont approximativement ind√©pendants les uns des autres, mais il est difficile de trouver cette relation. On utilise ces nombres pseudo al√©atoires, car il est d'une part difficile d'obtenir des vrais nombres al√©atoires et d'autre part, ces algorithmes se pr√™tent bien √† une r√©alisation informatique. Une remarque c√©l√®bre de John Von Neumann¬†: Quiconque consid√®re des m√©thodes arithm√©tiques pour produire des nombres al√©atoires est, bien s√Ľr, en train de commettre un p√©ch√©. Des nombres pseudo al√©atoires ne sont pas des nombres al√©atoires, mais ils suffisent la plupart du temps.
- Les générateurs physiques de nombres aléatoires. Ces générateurs reposent sur le caractère quantique et donc aléatoire de certains phénomènes physiques comme le bruit thermique d'une résistance ou alors la radio activité ambiante.
Il est possible de trouver des g√©n√©rateurs de nombres al√©atoires reposant sur un ph√©nom√®ne physique chez Westphal Electronic. Celui pr√©sent√© ci-dessus coute 595 ‚ā¨.
Dans ce paragraphe nous étudierons exclusivement les générateurs de nombres pseudo aléatoires.
Les principaux générateurs de nombres aléatoires peuvent être du type :
- des générateurs linéaires congruents ;
- des générateurs à base de registre à décalage ;
- d'autres algorithmes spécifiques.
IX-A. Les g√©n√©rateurs lin√©aires congruents▲
Un générateur linéaire congruent est de la forme : dans lequel a, b et m sont les paramètres du générateur. Ce générateur a une période qui ne peut être plus grande que m et si a, b et m sont choisis correctement (par exemple b et m premiers entres eux), alors la période de répétition sera maximale et tous les nombres de la période seront utilisés.
Le générateur le plus connu est celui de la fonction rand() sur les machines IBM et d'autres machines 32 bits : . Mais ce générateur souffre d'un grave défaut, les nombres générés sont prévisibles, car il y a un lien entre Xn, Xn+1 et Xn+2. Les 3 valeurs consécutives sont liées par la formule :
.
Le tableau suivant présente quelques valeurs possibles pour les paramètres a, b et m :
|
a |
b |
n |
|---|---|---|
|
106 |
1 283 |
6 075 |
|
171 |
11 213 |
53 125 |
|
421 |
17 117 |
81 000 |
|
741 |
66 037 |
312 500 |
|
3 613 |
45 289 |
214 326 |
|
9 301 |
49 297 |
233 280 |
Ce type de générateur convient très bien pour des jeux, mais certainement pas en cryptographie, car l'espace des nombres obtenus est bien trop petit et en plus, les nombres obtenus sont trop prévisibles ?
- Quand on conna√ģt deux nombres, il est possible de retrouver les param√®tres du g√©n√©rateur.
- Quand on conna√ģt les param√®tres de ce g√©n√©rateur et un nombre, le nombre suivant se d√©duit tr√®s facilement.
IX-B. Les g√©n√©rateurs √† base de registre √† d√©calage▲
La notion de registre à décalage est issue de l'électronique. Dans ce composant, le registre contient un certain nombre de bits et à chaque impulsion d'horloge, tous les bits sont décalés d'une case vers la droite. Le bit le plus à droite est donc extrait du registre à décalage et un nouveau bit est inséré dans la partie gauche du registre.

La forme la plus simple de ce type de générateur est le registre à décalage à rétroaction linéaire encore appelé RDRL. La fonction de rétroaction est composée d'un ou exclusif qui n'utilise que quelques bits du registre à décalage.
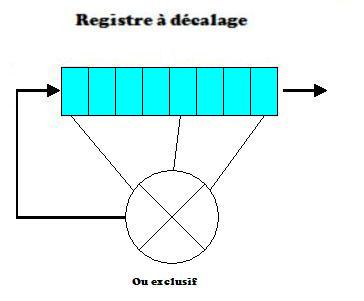
Le choix des bits √† utiliser dans la fonction de r√©tro action ne se fait pas au hasard. Pour que la fr√©quence soit maximale et que le g√©n√©rateur passe par tous les √©tats du registre √† d√©calage, il faut que le polyn√īme de r√©troaction (x^7+x^3+x^0 dans l'exemple ci-dessus) soit un polyn√īme primitif modulo 2 (un polyn√īme est dit primitif si le pgcd de tous ses coefficients est 1).
La liste suivante pr√©sente quelques polyn√īmes primitifs¬†:
- x^1 + x^0
- x^3 + x^1 + x^0
- x^7 + x^1 + x^0
- x^7 + x^3 + x^0
- x^12 + x^6 + x^4 + x^0
- x^14 + x^5 + x^3 + x^1 + x^0
L'exemple présenté ci-dessus génère un flux de bits. Pour générer un flux d'octets, il suffit de lire 8 bits et de les réassembler dans un octet ou encore de coupler 8 générateurs en parallèle afin de générer les 8 bits simultanément.
IX-C. L'algorithme BBS▲
L'algorithme Blum Blum Shub (BBS) du nom de ces inventeurs Lenore Blum, Manuel Blum et Michael Shub est un générateur de nombres pseudo aléatoires utilisable en cryptographie. Il fut inventé en 1986 et il repose sur la formule :
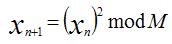
Avec M produit de deux nombres premiers congruent à 3 modulo 4. La sortie de l'algorithme est alors le bit de poids faible de chaque itération.
Cet algorithme est relativement lent (1 bit √† chaque it√©ration seulement), mais il est montr√© comme cryptographiquement s√Ľr.
IX-D. D'autres algorithmes▲
Il existe encore d'autres algorithmes de génération de nombres pseudo aléatoires parmi lesquels, on peut citer :
- Yarrow
- Fortuna
- ISSAC
X. Quelques applications de la cryptographie▲
Après ce survol des principaux algorithmes utilisés en cryptographie, nous allons voir dans ce paragraphe leurs utilisations pratiques.
Après les deux paragraphes sur les algorithmes symétriques et asymétriques, on serait tenté de penser que vu la souplesse dans d'utilisation des algorithmes asymétriques avec des clés publiques et privées, on pourrait oublier les algorithmes symétriques pour lesquels l'échange de clés est un réel problème.
Il n'en est rien, car les algorithmes asymétriques sont 100 à 1000 fois moins rapides que les algorithmes symétriques. C'est normal, car les opérations de manipulation de bits et de ou exclusif sur des nombres de 64 bits sont plus rapides que l'élévation à la puissance et la division de nombres de 1000 bits et plus.
En général, les algorithmes applicatifs vont utiliser les deux types d'algorithmes. La première phase utilisera un algorithme asymétrique pour échanger une clé (appelée clé de session) et ensuite, on passera en mode algorithme symétrique en utilisant cette clé de session négociée afin de pouvoir travailler plus vite.
On voit donc que la r√©sistance de ces algorithmes √† la cryptanalyse n'est pas le produit de la r√©sistance des deux algorithmes, mais plut√īt la valeur du plus faible des algorithmes utilis√©s. Il suffit que l'un des deux algorithmes soit faible (quelle qu'en soit la raison) pour que la session compl√®te soit faible.
X-A. PGP▲
PGP, pour Pretty Good Privacy, est un logiciel de chiffrement inventé en 1991 par Philip Zimmermann. Le but de ce logiciel est essentiellement de permettre l'échange de messages par messagerie électronique de manière totalement sécurisée. Ce logiciel aura causé beaucoup de soucis Philip Zimmermann pour deux raisons :
- un premier problème juridique avec la société RSA Data Security Inc, car le logiciel utilise la cryptographie RSA sans licence d'utilisation ;
- un second problème concernait le fait que la cryptographie et donc la sécurité des échanges de son logiciel était trop forte par rapport aux lois d'utilisation et d'exportations américaines.
Finalement en 1996 le problème s'est résolu par un accord négocié entre RSA Data Security Inc Philip Zimmermann et par l'abandon des poursuites du gouvernement américain. Entre temps, le logiciel et ses sources avaient été diffusés sur Internet.
Le logiciel PGP est un algorithme hybride dans le sens o√Ļ il utilise les deux techniques de cryptographie, la cryptographie sym√©trique et la cryptographie asym√©trique.
Le logiciel PGP propose les fonctionnalités suivantes.
- Chaque utilisateur de PGP possède une bi-clé RSA asymétrique. Cette bi-clé est composée d'une clé publique et d'une clé privée.
- Le logiciel PGP permet de stocker la bi-clé avec une sécurité supplémentaire pour l'archivage de la clé privée, elle est protégée par une phrase que l'utilisateur doit entrer pour la déverrouiller la clé privée.
- Le logiciel permet d'importer les clés publiques des autres usagers avec qui l'utilisateur communique habituellement dans son porte-clés.
- Le logiciel permet de chiffrer un message à destination d'un ou plusieurs des usagers dont les clés publiques sont dans le porte-clés PGP.
- Le logiciel permet de déchiffrer les messages reçus en utilisant la clé privée de l'utilisateur (après déverrouillage).
- Le logiciel permet de signer un message et de l'envoyer. Ainsi, le destinataire peut √™tre s√Ľr de l'√©metteur.
- Le logiciel permet de vérifier la signature d'un message.
Le gros problème de PGP concerne la vérification que la clé publique de Bernard est bien celle de Bernard et pas celle d'Estelle qui voudrait usurper l'identité de Bernard. Ce problème est partiellement et incomplètement résolu par la signature des clés.
Si Bernard fait signer sa cl√© par Christine et David et qu'Alice conna√ģt Christine ou David, intuitivement elle pourra penser que la cl√© de Bernard est plus valide que si cette cl√© n'√©tait sign√©e par personne. Il y a transfert de la confiance.
PGP peut être librement téléchargé. Il existe aussi la version GnuPG qui respecte la licence GNU General Public License.
X-B. Notion de Certificat▲
Avec PGP, Philip Zimmermann a résolu d'une certaine manière le problème de la confiance accordée à une clé publique. Cette confiance est transmise de proche en proche par la signature de la clé par un intermédiaire.
Un probl√®me se pose si Alice et Bernard veulent s'√©changer de mani√®re s√©curis√©e des messages et qu'ils n'ont pas d'interm√©diaires capables de valider les cl√©s publiques ou si la cha√ģne des interm√©diaires est tellement longue que la confiance que l'on peut accorder √† cette cha√ģne d'interm√©diaires est faible.
Ce problème est résolu par la notion de certificat. Alice et Bernard font tous les deux confiance à une autorité de certification et cette autorité valide les clés publiques d'Alice et Bernard. Encore une fois, le problème est de faire confiance à cette autorité de certification, mais de toute façon, à un moment ou à un autre, il va falloir faire confiance à quelque chose ou à quelqu'un.
Un certificat peut être vu comme une enveloppe qui accompagne la clé publique. Cette enveloppe est signée par l'autorité de certification. Toute falsification de cette enveloppe pourra être détectée, car lorsque le destinataire du certificat vérifiera la signature du certificat, il se rendra compte qu'elle n'est pas valide.
Une norme, la norme X.509, spécifie le contenu d'un certificat. On parlera alors de certificats X.509.
Voyons maintenant quels sont les éléments contenus dans un certificat X.509.
- La version de la norme utilisée par le certificat. La norme X.509 a évolué et il en existe maintenant 3 versions différentes.
- Un numéro de série. Ce numéro de série est unique pour une autorité de certification donnée.
- Le nom de l'autorité de certification.
- La période de validité de ce certificat. Hors de cette période, un certificat est invalide.
- L'identification du possesseur de la clé publique.
- L'identification de l'algorithme de la clé publique ainsi que la clé publique de la personne.
- Des informations complémentaires optionnelles.
- L'identification de l'algorithme et la valeur de la signature du certificat.
Il existe quatre classes de certificat. Ces quatre classes sont définies en fonction du niveau de sécurité du processus utilisé lors de la génération du certificat.
- Classe 1 : L'adresse mail du demandeur suffit pour créer ce type de certificat.
- Classe 2 : Preuve d'identité requise (carte d'identité, extrait de Kbis pour les entreprises, etc.).
- Classe 3 : C'est un certificat de classe 2, mais la présence physique du demandeur est requise.
- Classe 4 : C'est un certificat de classe 3, mais celui-ci est implanté directement sur un support de type carte à puce.
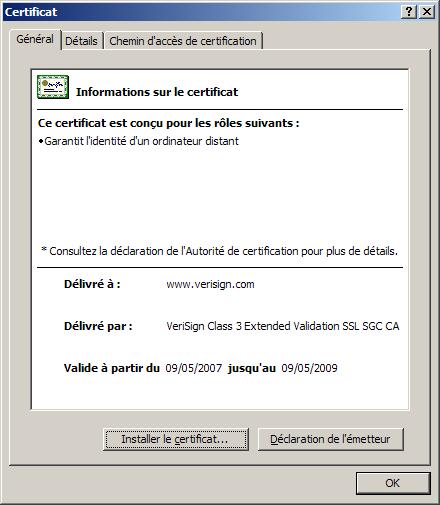
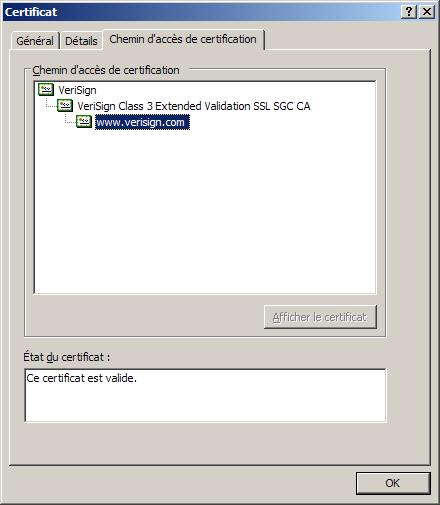
Le certificat suivant est celui obtenu lorsque l'on se connecte sur le site de VeriSign :
Les informations que l'on retrouve dans ce certificat sont :
- Version X.509 utilisée : 3
- Numéro de série du certificat : 6a 4a c3 1b 31 10 e6 eb 48 f0 fc 51 a3 9a 17 1f
- Algorithme de signature : Sha-1 et RSA
-
Identification de l'autorité de certification : VeriSign Class 3 Extended Validation SSL SGC CA
- CN = VeriSign Class 3 Extended Validation SSL SGC CA
- OU = Terms of use at https://www.verisign.com/rpa (c)06
- OU = VeriSign Trust Network
- O = VeriSign, Inc., C=US
- Valide depuis le mercredi 9 mai 2007 01:00:00
- Valide jusqu'au samedi 9 mai 2009 00:59:59 (période de validité : 2 ans)
-
Identification du propriétaire de la clé publique : www.verisign.com
- CN = www.verisign.com
- OU = Terms of use at www.verisign.com/rpa (c)06
- OU = Production Security Services
- O = VeriSign, Inc.
- STREET = 487 East Middlefield Road
- L = Mountain View
- S = California
- PostalCode = 94043
- C = US
- 1.3.6.1.4.1.311.60.2.1.2 = Delaware
- 1.3.6.1.4.1.311.60.2.1.3 = US
- Clé publique : Algorithme RSA, clé publique de 1024 bits, valeur de la clé publique : 30 81 89 02 81 81 00 c7 10 37 e5 eb fc ef d7 6b 81 00 a9 10 d1 91 43 70 11 68 23 f3 fd 69 de 4f d7 6d 31 ed ea 18 db f3 5d 02 6c e9 c8 e6 d4 1c 7c 5d e8 32 5b 58 01 8c 95 f9 66 5e 16 59 ba fd c2 90 16 67 56 32 27 46 c4 c9 28 48 1a 69 14 f1 f3 df 6d c5 d8 c1 2c 96 a1 6c 2f 13 93 51 69 40 76 ce d9 9f 01 57 6f 39 a1 8c 50 ac 67 cb 60 e7 8f 7b 40 75 a4 3e 14 e7 91 0c 92 58 83 a2 b5 87 37 33 ab fa 2d 39 fb 02 03 01 00 01
-
Quelques informations concernant le domaine d'utilisation possible de ce certificat
- Contrainte de base : Type d'objet=Entité finale, Contrainte de longueur de chemin d'accès=Aucun(e)
- Identificateur de la clé du sujet : f1 5a 89 93 55 47 4b ba 51 f5 4e e0 cb 16 55 f4 d7 cc 38 67
- Utilisation de la clé : Signature numérique, Cryptage de la clé (a0)
- Point de distribution de la liste de révocation des certificats : URL=http://EVIntl-crl.verisign.com/EVIntl2006.crl
- Stratégie de certificat : Identificateur de stratégie=2.16.840.1.113733.1.7.23.6
- Utilisation avancée de la clé : Authentification du serveur (1.3.6.1.5.5.7.3.1), Authentification du client (1.3.6.1.5.5.7.3.2), Utilisation de clé inconnue (2.16.840.1.113730.4.1), Utilisation de clé inconnue (1.3.6.1.4.1.311.10.3.3)
- Identification de la clé de l'autorité : 4e 43 c8 1d 76 ef 37 53 7a 4f f2 58 6f 94 f3 38 e2 d5 bd df
- Accès aux informations de l'autorité : Protocole d'état de certificat en ligne (1.3.6.1.5.5.7.48.1), Autorité de certification émettrice (1.3.6.1.5.5.7.48.2)
- 1.3.6.1.5.5.7.1.12 : Type d'information inconnue.
- Algorithme d'empreinte numérique : SHA-1
- Empreinte numérique du certificat : c6 75 0e 8d a9 5f 5a 65 bb 04 6d 60 79 d4 fc 87 40 2e 03 81
Il est aussi possible de conna√ģtre le chemin de certification du certificat¬†:
Le certificat de VeriSign est signé par le certificat VeriSign Class 3 Public Primary Certification Authority - G5 lui-même signé par le certificat racine de confiance Verisign.
X-C. Notions de PKI▲
Une PKI (en anglais Public Key Infrastructure) ou une IGC (en français Infrastructure de Gestion des Clés) est un ensemble de logiciels, machines et procédures permettant de gérer des certificats.
X-C-1. Les r√īles d'une PKI▲
Les services attendus d'une PKI sont les suivants.
- Création des certificats (enregistrement des utilisateurs ou des équipements informatiques, vérification des données d'identification, cohérence de ces informations).
- Gestion des certificats (publication, renouvellement, révocation).
- Gestion et publication de la liste des certificats révoqués (on parle aussi de listes de révocation).
- Identification et authentification des utilisateurs accédant à la PKI.
- Archivage, séquestre et recouvrement des certificats.
X-C-2. Les entit√©s d'une PKI▲
Une PKI définit cinq entités.
- L'autorité de certification dont le but est de signer les demandes de certificats et la liste des certificats révoqués. Cette autorité est la plus critique.
- L'autorité d'enregistrement dont le but est de générer les demandes de certificats après une éventuelle vérification d'identité du demandeur.
- L'autorit√© de d√©p√īt dont le but est de publier les certificats ainsi que les listes de r√©vocation.
- L'entité finale qui est l'utilisateur final ou la machine qui va utiliser le certificat.
- L'autorit√© de s√©questre dont le r√īle est de stocker de mani√®re s√©curis√©e les cl√©s priv√©es des certificats sign√©s par l'autorit√© de certification. Ce r√īle est optionnel et peut √™tre rendu obligatoire par la l√©gislation de certains pays (dont la France) qui imposent de fournir aux autorit√©s un moyen permettant de d√©chiffrer les donn√©es chiffr√©es par un certificat.
X-C-3. L'autorit√© de certification▲
L'autorité de certificat est l'organisme ou l'entité qui signe les demandes de certificats émises par les usagers.
La signature d'un certificat par une autorité de certification permet d'apporter la crédibilité et la confiance que l'on a en cette autorité de certification sur un certificat.
Cette signature permet aussi de garantir que les informations transportées dans ce certificat ne sont pas modifiées ni altérées. Un usager ne peut pas modifier son certificat ou s'il le fait, cela sera immédiatement détecté, car la signature du certificat ne correspondra plus avec celle générée par l'autorité de certification.
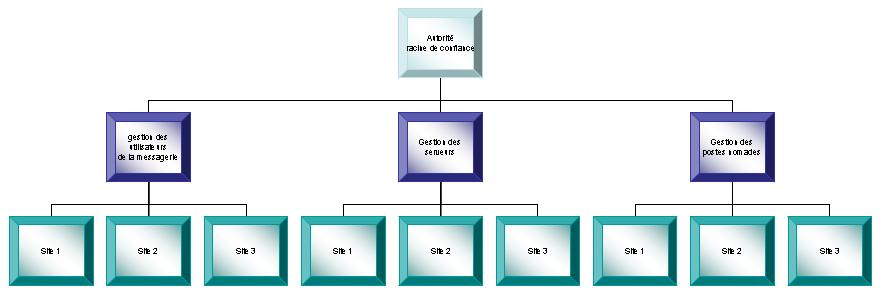
Il arrive souvent que l'autorité de certification soit hiérarchisée et déléguée. Il est courant dans les entreprises de trouver une architecture à plusieurs niveaux :
Dans cet exemple, on trouve une autorité de certification racine qui signe les certificats des autorités de certification de gestion des utilisateurs de la messagerie, de gestion des serveurs et de gestion des postes nomades. Chacune de ces trois entités signe à son tour un certificat pour chacun des trois sites de l'entreprise.
Finalement, les certificats des usagers seront signés par une autorité de certification locale au site dont la mission est déléguée depuis l'autorité racine de confiance par les certificats intermédiaires.
X-D. SSL▲
SSL (pour Secure Socket Layer) est un protocole réseau de chiffrement. La première version de ce protocole a été développée par Netscape pour assurer la sécurité des échanges sur Internet lors des phases sensibles (paiement sécurisé entres autres).
Les différentes versions de SSL sont les versions 1.0 et 2.0. La version actuelle est la version 3.0 et la version 3.1 correspond à la version TLS 1.0 standardisée par l'IETF (Internet Engineering Task Force). TLS (Transport Layer Security) est décrit dans la RFC 2246.
SSL est totalement transparent par rapport aux données transportées. Il ne peut s'appuyer que sur les protocoles TCP.
Le protocole SSL définit en fait trois sous protocoles.
- Le protocole Handshake
- Le protocole Change cipher spec
- Le protocole Alert
X-D-1. Le protocole Handshake▲
Ce protocole permet de vérifier l'authentification obligatoire du serveur et l'authentification facultative du client. Elle permet de spécifier la clé de session qui sera utilisée lors des échanges sécurisés. Elle permet aussi de négocier les algorithmes utilisés lors de la phase de chiffrement.
Les messages possibles lors du protocole Handshake sont :
- hello_request (valeur 0)
- client_hello (valeur 1)
- server_hello (valeur 2)
- certificate (valeur 11)
- server_key_exchange (valeur 12)
- certificate_request (valeur 13)
- server_hello_done (valeur 14)
- certificate_verify (valeur 15)
- client_key_exchange (valeur 16)
- finished (valeur 20)
X-D-2. Le protocole Change cipher spec▲
Ce protocole comprend en fait un seul message qui permet au protocole SSL d'utiliser les algorithmes négociés lors de la phase Handshake du protocole et de passer en mode chiffré.
Le seul message possible lors du protocole Change cipher spec est :
- change_cipher_spec(valeur 1)
X-D-3. Le protocole Alert▲
Le protocole Alert est le protocole qui permet de remonter les messages d'erreur protocolaires.
Les messages possibles lors du protocole Alert peuvent avoir 2 niveaux : Warning ou Fatal. Les messages d'alerte sont :
- close_notify (valeur 0)
- unexpected_message (valeur 10)
- bad_record_mac (valeur 20)
- decryption_failed (valeur 21)
- record_overflow (valeur 22)
- decompression_failure (valeur 30)
- handshake_failure (valeur 40)
- bad_certificate (valeur 42)
- unsupported_certificate (valeur 43)
- certificate_revoked (valeur 44)
- certificate_expired (valeur 45)
- certificate_unknown (valeur 46)
- illegal_parameter (valeur 47)
- unknown_ca (valeur 48)
- access_denied (valeur 49)
- decode_error (valeur 50)
- decrypt_error (valeur 51)
- export_restriction (valeur 60)
- protocol_version (valeur 70)
- insufficient_security (valeur 71)
- internal_error (valeur 80)
- user_canceled (valeur 90)
- no_renegotiation (valeur 100)
X-D-4. La phase de n√©gociation du protocole Handshake▲
Les échanges protocolaires entre le client SSL et le serveur SSL sont synthétisés dans le tableau suivant :
|
Client |
Serveur |
|---|---|
|
ClientHello |
|
|
ServerHello |
|
|
Certificate (optionnel) |
|
|
ChangeCipherSpec |
|
|
Application Data |
Application Data |
Il existe aussi un protocole Handshake simplifié qui permet de reprendre le protocole sur erreur ou aussi de dupliquer une session SSL. L'échange protocolaire est alors :
|
Client |
Serveur |
|---|---|
|
ClientHello |
|
|
ServerHello |
|
|
ChangeCipherSpec |
|
|
Application Data |
Application Data |
On trouvera tous les détails de spécification du protocole dans la RFC 2246.
X-D-5. Les algorithmes n√©goci√©s par SSL▲
Les combinaisons d'algorithmes négociables par SSL sont les suivantes :
|
Algorithme asymétrique |
Algorithme symétrique |
Algorithme d'empreinte |
|---|---|---|
|
RSA |
Aucun |
MD5 |
|
RSA |
Aucun |
SHA |
|
RSA export |
RC4 40 bits |
MD5 |
|
RSA |
RC4 128 bits |
MD5 |
|
RSA |
RC4 128 bits |
SHA |
|
RSA export |
RC2 40 bits mode CBC |
MD5 |
|
RSA |
IDEA mode CBC |
SHA |
|
RSA export |
DES 40 bits mode CBC |
SHA |
|
RSA |
DES mode CBC |
SHA |
|
RSA |
3DES EDE mode CBC |
SHA |
|
DH et DSS export |
DES 40 bits mode CBC |
SHA |
|
DH et DSS |
DES mode CBC |
SHA |
|
DH et DSS |
3DES EDE mode CBC |
SHA |
|
DH et RSA export |
DES 40 bits mode CBC |
SHA |
|
DH et RSA |
DES mode CBC |
SHA |
|
DH et RSA |
3DES EDE mode CBC |
SHA |
|
DHE et DSS export |
DES 40 bits mode CBC |
SHA |
|
DHE et DSS |
DES mode CBC |
SHA |
|
DHE et DSS |
3DES EDE mode CBC |
SHA |
|
DHE et RSA export |
DES 40 bits mode CBC |
SHA |
|
DHE et RSA |
DES mode CBC |
SHA |
|
DHE et RSA |
3DES EDE mode CBC |
SHA |
|
DH anonyme export |
RC4 40 bits |
MD5 |
|
DH anonyme |
RC4 128 bits |
MD5 |
|
DH anonyme export |
DES 40 bits mode CBC |
SHA |
|
DH anonyme |
DES mode CBC |
SHA |
|
DH anonyme |
3DES EDE mode CBC |
SHA |
X-D-6. Les ports utilis√©s par SSL▲
Les principaux protocoles transportés par SSL et les ports utilisés par défaut sont :
|
Protocole |
Port par défaut |
Port SSL par défaut |
|---|---|---|
|
HTTP |
80 |
443 |
|
SMTP |
25 |
465 |
|
NNTP |
119 |
563 |
|
POP3 |
110 |
995 |
|
IMAP |
143 |
993 |
|
TELNET |
23 |
992 |
X-E. OpenSSL▲
OpenSSL est un projet collaboratif dont le but est d'offrir une implémentation d'algorithmes liés à la cryptographie.
Tous les algorithmes ne sont pas implémentés principalement pour des raisons de licences non compatibles avec la licence OpenSSL.
Le projet se compose de deux éléments principaux :
- une bibliothèque écrite en C ;
- une interface ligne de commande.
À la date de rédaction de ce document, la dernière version OpenSSL est la version 0.9.8j du 7 janvier 2009.
X-E-1. Contenu de la biblioth√®que▲
Les fonctionnalités implémentées dans la bibliothèque OpenSSL sont :
- Algorithmes symétriques : blowfish, cast, des, idea, rc2, rc4, rc5,
- Algorithmes asymétriques : dsa, dh, rsa,
- Algorithme de hash : hmac, md2, md4, md5, mdc2, ripemd, sha,
- Gestion des certificats : x509, x509v3,
- Gestion des encodages : asn1, bio, evp, pem, pkcs#7, pkcs#12
Cette bibliothèque permet aux programmes qui le souhaitent d'utiliser des fonctions cryptographiques de manière simple et éprouvée à l'aide d'une API très documentée.
X-E-2. L'interface ligne de commande▲
L'interface ligne de commande d'OpenSSL permet d'utiliser la bibliothèque OpenSSL et tous ses algorithmes. Il est possible par le biais de l'interface ligne de commande de créer un certificat X.509, de signer ce certificat, de chiffrer un fichier en utilisant un algorithme particulier et une clé donnée, de déchiffre un fichier, de calculer le code de hachage d'un fichier, et beaucoup d'autres choses encore.
Une autre possibilité de cette interface ligne de commande est qu'il est possible de lancer un serveur SSL à l'écoute sur un port particulier ou un client SSL qui va se connecter sur un serveur SSL. Cette fonctionnalité est très utile pour le débogage des applications.
X-F. Crypto++▲
Crypto++ est un autre projet collaboratif dont le but est d'offrir une implémentation d'algorithmes liés à la cryptographie.
Comme son nom l'indique, il s'agit d'une bibliothèque de classes C++. La dernière version de cette bibliothèque est la version 5.5.2 du 24 septembre 2007.
Les algorithmes implémentés par cette bibliothèque sont :
|
high speed stream ciphers |
Panama, Salsa20, Sosemanuk |
|
AES and AES candidates |
AES (Rijndael), RC6, MARS, Twofish, Serpent, CAST-256 |
|
other block ciphers |
IDEA, Triple-DES (DES-EDE2 and DES-EDE3), Camellia, RC5, Blowfish, TEA, XTEA, Skipjack, SHACAL-2 |
|
block cipher modes of operation |
ECB, CBC, CBC ciphertext stealing (CTS), CFB, OFB, counter mode (CTR) |
|
message authentication codes |
VMAC, HMAC, CBC-MAC, DMAC, Two-Track-MAC |
|
hash functions |
SHA-1, SHA-2 (SHA-224, SHA-256, SHA-384, and SHA-512), Tiger, WHIRLPOOL, RIPEMD-128, RIPEMD-256, RIPEMD-160, RIPEMD-320 |
|
public-key cryptography |
RSA, DSA, ElGamal, Nyberg-Rueppel (NR), Rabin, Rabin-Williams (RW), LUC, LUCELG, DLIES (variants of DHAES), ESIGN |
|
padding schemes for public-key systems |
PKCS#1 v2.0, OAEP, PSS, PSSR, IEEE P1363 EMSA2 and EMSA5 |
|
key agreement schemes |
Diffie-Hellman (DH), Unified Diffie-Hellman (DH2), Menezes-Qu-Vanstone (MQV), LUCDIF, XTR-DH |
|
elliptic curve cryptography |
ECDSA, ECNR, ECIES, ECDH, ECMQV |
|
insecure or obsolescent algorithms retained for backwards compatibility and historical value |
MD2, MD4, MD5, Panama Hash, DES, ARC4, SEAL 3.0, WAKE, WAKE-OFB, DESX (DES-XEX3), RC2, SAFER, 3-WAY, GOST, SHARK, CAST-128, Square |
Les autres fonctionnalités de la bibliothèque sont :
- pseudo random number generators (PRNG): ANSI X9.17 appendix C, RandomPool
- password based key derivation functions: PBKDF1 and PBKDF2 from PKCS #5, PBKDF from PKCS #12 appendix B
- Shamir's secret sharing scheme and Rabin's information dispersal algorithm (IDA)
- fast multiprecision integer (bignum) and polynomial operations
- finite field arithmetics, including GF(p) and GF(2^n)
- prime number generation and verification
-
useful non-cryptographic algorithms
- DEFLATE (RFC 1951) compression/decompression with gzip (RFC 1952) and zlib (RFC 1950) format support
- hex, base-32, and base-64 coding/decoding
- 32-bit CRC and Adler32 checksum
-
class wrappers for these operating system features (optional) :
- high resolution timers on Windows, Unix, and Mac OS
- Berkeley and Windows style sockets
- Windows named pipes
- /dev/random, /dev/urandom, /dev/srandom
- Microsoft's CryptGenRandom on Windows
- A high level interface for most of the above, using a filter/pipeline metaphor
- benchmarks and validation testing
-
x86, x86-64 (x64), MMX, and SSE2 assembly code for the most commonly used algorithms, with run-time CPU feature detection and code selection
- supports GCC-style and MSVC-style inline assembly, and MASM for x64
- certain versions are available in FIPS 140-2 validated form
XI. La cryptographie quantique▲
Jusqu'à présent, les différents algorithmes présentés reposaient en grande partie sur les mathématiques. Une nouvelle classe d'algorithmes est en train d'émerger : il s'agit de la cryptographie quantique.
Ces algorithmes ne sont plus bas√©s sur des principes math√©matiques, mais plut√īt sur les principes de la physique quantique.
La cryptographie quantique n'est pas vraiment un algorithme de chiffrement. Elle met en Ňďuvre l'algorithme de cryptographie du masque jetable qui est le seul algorithme dont l'absence de faille est prouv√©e (voir ou revoir le paragraphe 7.5).
Cet algorithme est tr√®s s√Ľr, mais il n√©cessite une cl√© al√©atoire partag√©e entre l'√©metteur et le r√©cepteur aussi longue que le message √† √©changer. L'√©change de cette cl√© fait que cet algorithme est peu facile √† utiliser.
XI-A. Propri√©t√©s quantiques d'un photon▲
La cryptographie quantique repose sur les propriétés quantiques du photon polarisé. La compréhension de ces propriétés est indispensable pour comprendre la cryptographie quantique.
- Un photon peut être polarisé selon un axe quelconque.
-
Un photon polarisé selon un angle ? passant au travers d'un filtre polarisant d'angle ? possède une chance égale à cos²(? - ?) de passer au travers de ce filtre polarisant. Donc :
- si le filtre est orienté précisément dans l'axe de polarisation du photon (? = ?), la probabilité que le photon traverse le filtre est cos²(? - ?) = cos²(0) = 1, c'est-à-dire qu'il traverse le filtre ;
- si le filtre est orient√© √† 90¬į de l'axe de polarisation du photon (? = ? + 90), la probabilit√© que le photon traverse le filtre est cos¬≤(? - ?) = cos¬≤(90) = 0, c'est-√†-dire qu'il est arr√™t√© par le filtre¬†;
- si le filtre est orient√© √† 45¬į de l'axe de polarisation du photon (? = ? + 45), la probabilit√© que le photon traverse le filtre est cos¬≤(? - ?) = cos¬≤(45) = 1/2, c'est-√†-dire que le photon a une chance sur deux de passer le filtre.
-
Ces propriétés sont encore du domaine dit de la physique classique. Les autres propriétés purement quantiques utilisées sont :
- quand la probabilité de passer au travers du filtre n'est ni 0 ni 1, le passage d'un photon individuel au travers du filtre polarisant est fondamentalement imprévisible et indéterministe ;
- on ne peut conna√ģtre l'axe de polarisation d'un photon qu'en le faisant passer au travers d'un filtre polarisant. Il n'existe pas de mesure directe permettant de mesurer l'angle de polarisation d'un photon¬†;
- on ne peut conna√ģtre l'axe de polarisation d'un photon qu'en utilisant un filtre polarisant dont l'axe de polarisation est exactement √† 0¬į ou √† 90¬į par rapport √† l'axe de polarisation du photon.
La table de vérité ci-dessous présente les probabilités qu'un photon passe au travers d'un filtre polarisant suivant les différents angles du photon (colonne de gauche) et suivant les différents angles de filtre (ligne du haut) :
|
Filtre polaris√© √† 0¬į |
Filtre polaris√© √† 45¬į |
Filtre polaris√© √† 90¬į |
Filtre polaris√© √† 135¬į |
|
|
Photon polaris√© √† 0¬į |
1 |
1/2 |
0 |
1/2 |
|
Photon polaris√© √† 45¬į |
1/2 |
1 |
1/2 |
0 |
|
Photon polaris√© √† 90¬į |
0 |
1/2 |
1 |
1/2 |
|
Photon polaris√© √† 135¬į |
1/2 |
0 |
1/2 |
1 |
XI-B. Transmission de la cl√©▲
La transmission de la clé consiste à transmettre une série de bits aléatoires prenant comme valeur 0 ou 1. Alice transmet chaque bit en choisissant aléatoirement un des deux modes de polarisation possibles :
- le mode de polarisation rectiligne consiste √† envoyer un photon polaris√© √† 0¬į pour un bit 0 et √† 90¬į pour un bit 1¬†;
- le mode de polarisation diagonale consiste √† envoyer un photon polaris√© √† 45¬į pour un bit 0 et √† 135¬į pour un bit 1.
Alice émet chaque bit de la clé, photon par photon en notant pour chaque photon envoyé et donc pour chacun des bits le mode de polarisation choisi.
Bernard dispose d'un filtre polarisant pouvant √™tre orient√© au choix √† 0¬į et 180¬į) (ceci correspond au mode de polarisation rectiligne) ou √† 45¬į et 135¬į (ceci correspond au mode de polarisation diagonale). Il positionne le filtre al√©atoirement selon 1 des 2 modes possibles. Lors de l'arriv√©e d'un photon, il note le r√©sultat, c'est-√†-dire si le photon a pass√© ou non le filtre ainsi que le mode de polarisation qu'il avait choisi pour le filtre.
Pour chacun des photons reçus, il y a deux possibilités :
- Alice et Bernard ont par hasard choisi le même mode de polarisation. Dans ce cas, le photon reçu correspond au bit émis. Cela se produit en moyenne pour un photon sur deux ;
- Alice et Bernard ont choisi un mode de polarisation différent et dans ce cas le photon reçu est interprété de mauvaise manière. Cela se produit en moyenne pour un photon sur deux.
Une fois que tous les bits sont transmis, Alice communique à Bernard, par un moyen conventionnel et non forcément fiable, le mode de polarisation employé pour chacun des bits.
Bernard peut donc alors conna√ģtre les bits pour lesquels le mode de polarisation a √©t√© le m√™me. Il conna√ģt donc alors de mani√®re certaine N bits en moyenne pour 2xN bits transmis.
Par exemple :
Bits envoyés par Alice 1 1 0 0 1 0 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 1
Polarisation choisie par Alice + x + x + x + + + + x x x + x x x + x + x + + x + x x x + + x +
Polarisation choisie par Bernard + x x x + x + x + + x x + + + + x x x + x x + x x + x x + x + x
Valeurs lues par Bernard 1 1 0 0 1 0 1 0 1 1 1 1 0 1 0 0 1 0 0 1 1 0 1 0 0 0 1 0 1 0 0 0
Bits retenus 1 1 - 0 1 0 1 - 1 1 1 1 - 1 - - 1 - 0 1 1 - 1 0 - - 1 0 1 - - -Jusqu'ici, ce protocole n'est qu'une mani√®re (tr√®s compliqu√©e) de communiquer N bits entre Alice et Bernard. L'avantage de cette m√©thode est que Bernard peut avoir la certitude absolue que les photons et donc la cl√© n'ont pas √©t√© intercept√©s par Estelle. Un autre avantage non n√©gligeable est qu'Estelle ne peut jamais √™tre s√Ľre d'avoir bien intercept√© le message transmis par Alice.
Cela est possible, car, dans le cas o√Ļ l'on choisit une mauvaise orientation pour le filtre, la polarisation du photon re√ßu est parfaitement al√©atoire et ne donne aucune information sur sa polarisation initiale.
Estelle est oblig√©e, elle aussi, d'utiliser un filtre polarisant pour conna√ģtre la polarisation du photon qui code la valeur du bit. Pour passer inaper√ßue, Estelle doit r√©√©mettre le photon avec le m√™me √©tat de polarisation que le photon re√ßu. Mais si Estelle a choisi une mauvaise orientation du filtre pour recevoir le photon (cela arrive en moyenne une fois sur deux), elle va r√©√©mettre le photon avec une mauvaise polarisation.
Dans le cas o√Ļ Estelle intercepte des photons sur la ligne, il peut arriver des cas o√Ļ Bernard re√ßoit un bit diff√©rent du bit √©mis par Alice m√™me s'ils ont choisi le m√™me mode de polarisation.
Afin de tester la présence d'Estelle sur la ligne, Alice va, après avoir communiqué les modes de polarisation employés pour chaque photon, communiquer également la valeur de certains bits pour lesquels les orientations choisies par Alice et Bernard sont les mêmes.
Ces bits sont donc ¬ę¬†sacrifi√©s¬†¬Ľ puisqu'ils sont communiqu√©s par un canal de communication non s√Ľr. Maintenant, si un seul de ces bits diff√®re entre Alice et Bernard, ils peuvent √™tre s√Ľrs qu'Estelle a tent√© d'intercepter la cl√© et r√©agir en cons√©quence (abandon de la communication, choix d'un autre canal, etc.).
Ce concept d'√©change de cl√© a √©t√© invent√© en 1984 par les Canadiens Charles Bennet et Gilles Brassard. Il faudra attendre 1989 pour voir la premi√®re d√©monstration physique mettant en Ňďuvre ce concept.
XI-C. √Čtat actuel de la cryptographie quantique▲
Actuellement, m√™me si les concepts sont parfaitement connus, la cryptographie quantique n'en est qu'√† ses d√©buts du fait des difficult√©s technologiques √† la mettre en Ňďuvre.
Ce système a montré que des clés quantiques pouvaient être envoyées le long d'une fibre optique de 20 kilomètres avec un débit supérieur à 1 Mbit/s - une performance qui pourrait permettre à des utilisateurs de communiquer avec une sécurité totale à travers les réseaux informatiques (source Techno-Science du 13 octobre 2008).
XII. Conclusion▲
Voilà, ce rapide tout d'horizon de la cryptographie est maintenant terminé. Pour conclure, je voudrais ajouter quelques recommandations issues de mon expérience personnelle.
- La cryptographie est une science des math√©matiques complexe. Ne vous lancez pas dans la conception d'un algorithme inviolable si vous ne poss√©dez pas de solides bases en math√©matiques. Tous les algorithmes solides ont √©t√© invent√©s par des math√©maticiens, la cryptographie est une science o√Ļ l'amateurisme n'a plus sa place.
- Ne vous lancez pas dans l'implémentation d'un algorithme sans avoir de quoi le tester (un jeu de tests complet). En effet, il est parfois tentant de vouloir améliorer un algorithme et d'introduire alors un effet de bord qui fera qu'il ne fonctionne plus tout à fait pareil. Un nombre signé transformé en nombre non signé ou un entier 16 bits promu en entier 32 bits peut avoir de graves conséquences sur le fonctionnement de l'algorithme.
- Utilisez quand c'est possible les fonctionnalités de votre machine ou de votre système d'exploitation. La Crypto API de Windows ou encore OpenSSL sont des bibliothèques éprouvées aussi bien par les concepteurs que par les utilisateurs.
- Préférez l'utilisation des algorithmes publics dont les sources sont disponibles et qui ont été examinés et validés par des personnes extérieures à un algorithme privé et dont en fait vous ne savez rien si ce n'est que l'éditeur vous garantit qu'il est fiable.
Merci à _Mac_ pour le travail effectué lors de la relecture de ce document.
XIII. Annexes▲
XIII-A. Quelques livres▲
|
Cryptographie appliquée 2e édition écrit par Bruce Schneier et traduit par Laurent Viennot. Une référence en termes d'algorithmes. Nécessite tout de même quelques notions en mathématiques et aussi en développement. |
|
|
Merveilleux nombres premiers écrit par Jean-Paul Delahaye. Ce livre est essentiellement axé sur les nombres premiers (normal vu le titre), mais possède un chapitre complet et détaillé sur la cryptographie asymétrique. |
|
|
Histoire des codes secrets écrit par Simon Singh. Ce livre se lit comme un roman et est abordable par le commun des mortels avec un niveau de connaissances mathématiques normal. Il retrace l'évolution de la cryptographie depuis l'antiquité jusqu'à nos jours. |
|
|
Cryptography in C and C++ écrit par Michael Welschenbach. Ce livre, comme son nom l'indique, s'intéresse à la cryptographie en C et en C++. Il explique la cryptographie et les mécanismes mathématiques sous-jacents avec une approche spécifiquement dédiée aux développeurs. |
|
XIII-B. Quelques sites Internet▲
- Le portail Wikipédia concernant la cryptologie.
- Un site qui explique le fonctionnement de SSL.
- Le tutoriel Introduction à la cryptologie écrit par Denis Lapoire sur developpez.com.
XIII-C. Solution au courrier entre George Sand et Alfred de Musset▲
Pour la première lettre, il faut lire une ligne sur 2, ce qui donne :
Je suis très émue de vous dire que j'ai
toujours une envie folle de me faire
baiser et je voudrais bien que ce soit
par vous. Je suis prête à vous montrer mon
cul, et si vous voulez me voir aussi
toute nue, venez me faire une visite.
Je vous prouverai que je suis la femme
la plus profonde comme la plus étroite
dont vous puissiez rêver, puisque votre
bite est bien longue, bien dure et souvent
grosse. Accourrez donc vite et venez me la
mettre.Pour la réponse, il faut lire uniquement le premier mot de chaque ligne :
Quand
Voulez-vous
Vous
Que
Je
Couche
Avec
VousEt pour la réponse finale, il faut aussi lire uniquement le premier lot de chaque ligne :
Cette
Nuit